Giải bài 3 trang 120 Toán 8 Tập 1 SGK Cánh Diều

Đề bài:

Cho hình bình hành MNPQ có các góc khác 90°, MP cắt NQ tại I. Khi đó

A. IM = IN.      B. IM = IP.

C. IM = IQ.      D. IM = MP.

Phân tích và Hướng dẫn giải:

Để giải bài toán này, các em cần nhớ lại tính chất cơ bản về đường chéo của hình bình hành.

• Định nghĩa: Hình bình hành là tứ giác có các cạnh đối song song.

• Tính chất về đường chéo: Trong một hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường.

Trong bài toán này, hình bình hành $MNPQ$ có hai đường chéo là $MP$ và $NQ$, cắt nhau tại điểm $I$. Dựa vào tính chất trên, điểm $I$ sẽ là trung điểm của cả hai đường chéo. Từ đó, chúng ta có thể suy ra mối quan hệ về độ dài của các đoạn thẳng.

Lời giải chi tiết:

* Đáp án: B

Ta có hình minh hoạ như sau:

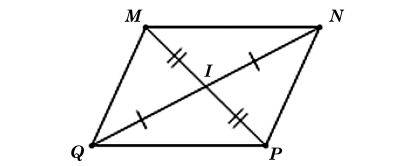
Hình bình hành MNPQ có hai đường chéo MP cắt NQ tại I nên I là trung điểm của mỗi đường.

Vì I là trung điểm của MP nên IM = IP.