Giải bài 4 trang 83 Toán 8 Tập 1 SGK Cánh Diều

Đề bài:

Một kho chứa có dạng hình chóp tam giác đều với độ dài cạnh đáy khoảng 12 m và độ dài trung đoạn khoảng 8 m (Hình 10). Người ta muốn sơn phủ bên ngoài cả ba mặt xung quanh của kho chứa đó và không sơn phủ phần làm cửa có diện tích là 5 m².

Biết rằng cứ mỗi mét vuông sơn cần trả 30 000 đồng. Cần phải trả bao nhiêu tiền để hoàn thành việc sơn phủ đó?

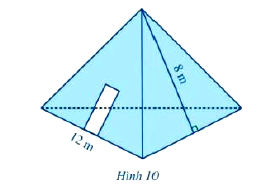
Phân tích và Hướng dẫn giải:

Để giải bài toán này, chúng ta cần thực hiện các bước sau:

1. Tính diện tích xung quanh: Kho chứa có hình dạng hình chóp tam giác đều, nên diện tích xung quanh sẽ bao gồm diện tích của ba mặt bên. Công thức tính diện tích xung quanh là , trong đó:

   S là diện tích xung quanh

   C là chu vi đáy

   d là độ dài trung đoạn của hình chóp tam giác đều

2. Tính diện tích cần sơn: Đề bài cho biết có một phần cửa không sơn với diện tích là m². Do đó, diện tích cần sơn sẽ bằng diện tích xung quanh trừ đi diện tích của phần cửa này.

3. Tính tổng chi phí: Sau khi có diện tích cần sơn, các em chỉ cần nhân diện tích đó với chi phí sơn cho mỗi mét vuông ( đồng) để tìm ra tổng số tiền phải trả.

Lời giải chi tiết:

* Diện tích xung quanh của hình chóp tam giác đều bằng nửa tích của chu vi đấy với độ dài trung đoạn.

* Áp dụng giải bài toán này:

- Chu vi đáy (đáy là tam giác đều) là: C = 3.12 = 36 (cm)

- Diện tích xung quanh của kho chứa hình chóp tam giác đều đó là:

- Diện tích cần sơn là:

144 – 5 = 139 (m²),

- Số tiền cần trả để hoàn thành việc sơn phủ đó là:

139 . 30 000 = 4 170 000 (đồng).