Toán 11 - Giới hạn của hàm số, cách tính và bài tập áp dụng
Chào các em! Giới hạn của hàm số là một trong những khái niệm nền tảng và quan trọng nhất của chương trình Toán 11. Nắm vững kiến thức này sẽ giúp các em giải quyết được nhiều dạng bài tập phức tạp, đặc biệt là các bài toán liên quan đến tính liên tục của hàm số.
Bài viết này sẽ tổng hợp một cách hệ thống và chi tiết về lý thuyết, các phương pháp giải và các dạng bài tập điển hình về giới hạn của hàm số.
A. Lý thuyết và các dạng Bài tập có lời giải chi tiết
I. Giới hạn hữu hạn
1. Giới hạn đặc biệt
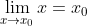
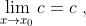 (c: hằng số)
(c: hằng số)
2. Định lý
a) Nếu: 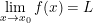 và
và 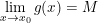 thì:
thì:
![small lim_{x
ightarrow x_{0}}[f(x)+g(x)]=L+M](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941830189y0r6m8g7d.gif)
![small lim_{x
ightarrow x_{0}}[f(x)-g(x)]=L-M](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594183019d3m6g42vv7.gif)
![small lim_{x
ightarrow x_{0}}[f(x).g(x)]=L.M](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594183021hh7kdqv700.gif)
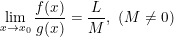
b) Nếu 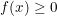 và
và 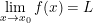 thì:
thì:
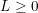 và
và 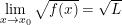
c) Nếu 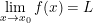 thì
thì 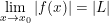
II. Giới hạn vô cực. Giới hạn ở vô cực
1. Giới hạn đặc biệt
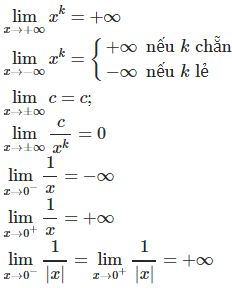
2. Định lý:

III. Giới hạn 1 bên
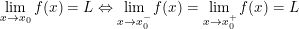
* Khi tính giới hạn có một trong các dạng vô định: 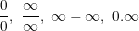 thì phải tìm cách khử dạng vô định.
thì phải tìm cách khử dạng vô định.
* Chú ý: Đối với các hàm lượng giác thì vận dụng tương tự với giới hạn khi x tiến tới vô cùng của sinx/x =1
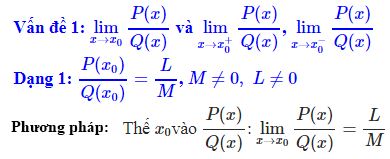
* Ví dụ 1: Tính giới hạn:
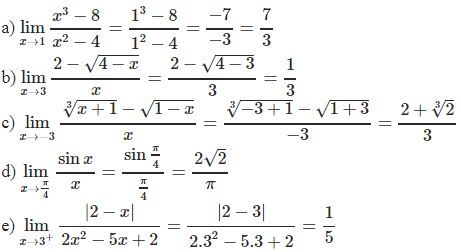
Bài tập vận dụng dạng 1:
¤ Bài tập 1: Tìm các giới hạn sau
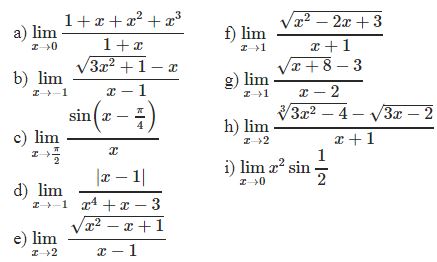
¤ Bài tập 2: Tìm các giới hạn sau
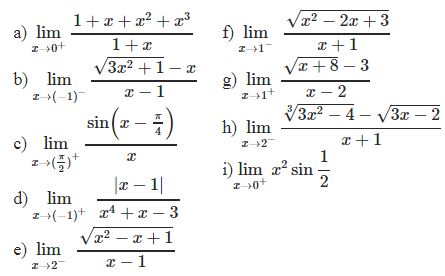
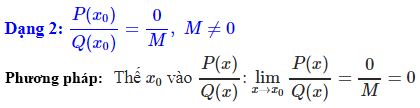
* Ví dụ 2: Tính các giới hạn
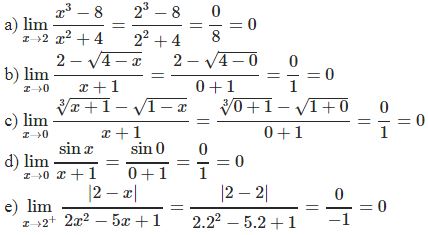
Bài tập vận dụng dạng 2:
¤ Bài tập 1: Tìm các giới hạn sau
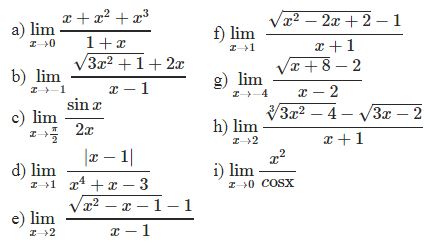
¤ Bài tập 2: Tìm các giới hạn sau
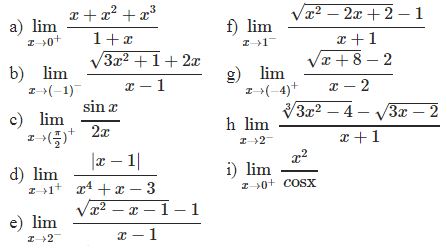
![]()
* Phương pháp: Áp dụng 2 quy tắc giới hạn vô cực (Quy tắc 1 & Quy tắc 2)
* Ví dụ 3: Tính giới hạn
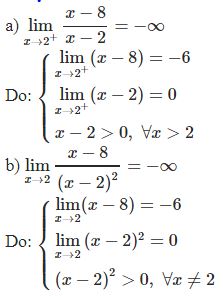
Bài tập vận dụng dạng 3:
¤ Bài tập 1: Tìm các giới hạn sau:
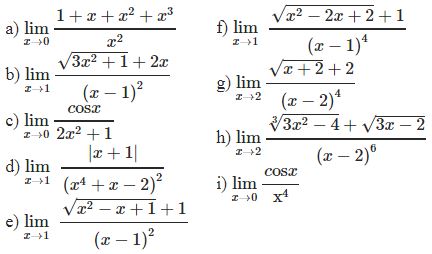
Bài tập 2: Tìm các giới hạn sau:
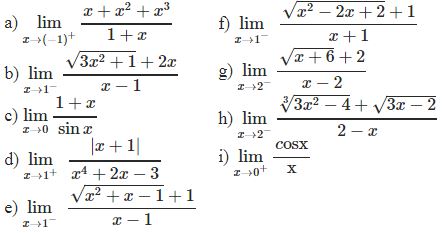
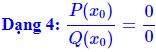
* Phương pháp:
- Nhóm các nhân tử chung: x - x0
- Nhân thêm lượng liên hợp
- Thêm, bớt số hạng vắng.
a) 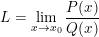 với
với 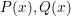 là các đa thức và
là các đa thức và 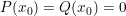
Ta phân tích cả tử và mẫu thành nhân tử và rút gọn.
* Ví dụ 4: Tính giới hạn:
• 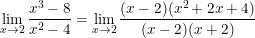
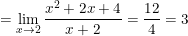
b) 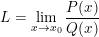 với
với 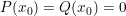 và
và 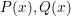 là các biểu thức chứa căn đồng bậc.
là các biểu thức chứa căn đồng bậc.
- Ta sử dụng các hằng đẳng thức để nhân lượng liên hợp ở tử thức và mẫu thức.
* Ví dụ 5: Tính giới hạn:
• 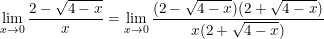
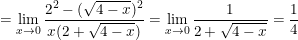
c) 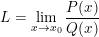 với
với 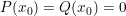 và
và 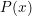 là biểu thức chứa căn không đồng bậc.
là biểu thức chứa căn không đồng bậc.
Giả sử: ![small P(x)=sqrt[m]{u(x)}-sqrt[n]{v(x)}](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594195247w6bmyncin3.gif) với
với ![small sqrt[m]{u(x_{0})}-sqrt[n]{v(x_{0})}=a](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/159419221735ygzqj4cl.gif)
Ta phân tích: ![small small P(x)=(sqrt[m]{u(x)}-a)+(a-sqrt[n]{v(x)})](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594195248s3pi7hilb4.gif)
* Ví dụ 6: Tìm giới hạn:
•![small lim_{x
ightarrow 0}frac{sqrt[3]{x+1}-sqrt{1-x}}{x} =lim_{x
ightarrow 0}left (frac{sqrt[3]{x+1}-1}{x}+frac{1-sqrt{1-x}}{x}
ight )](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941922210zguu2t0ra.gif)
![small =lim_{x
ightarrow 0}left (frac{1}{sqrt[3]{(x+1)^2}+sqrt[3]{x+1}+1}+frac{1}{1+sqrt{1-x}}
ight )](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594192222otwax094qa.gif)
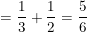
Bài tập vận dụng dạng 4:
¤ Bài tập 1: Tìm các giới hạn sau
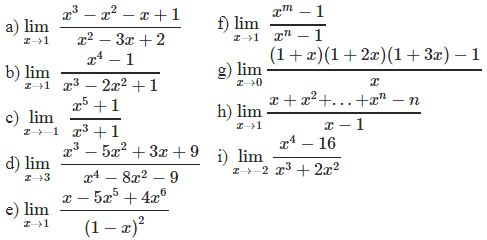
¤ Bài tập 2: Tìm các giới hạn sau
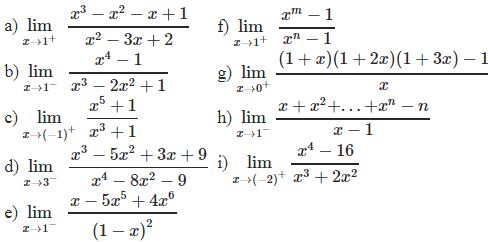
¤ Bài tập 3: Tìm các giới hạn sau
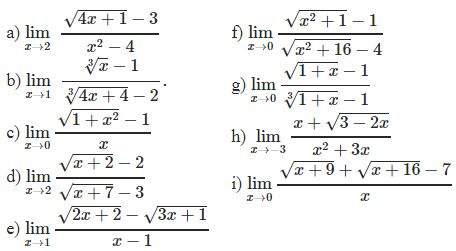
¤ Bài tập 4: Tìm các giới hạn sau
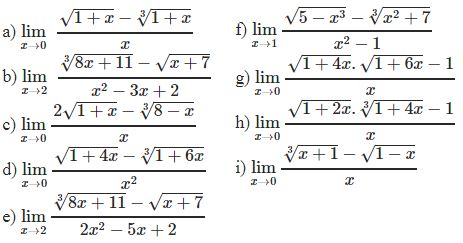
![]()
* Phương pháp: Ta cũng thường sử dụng các phương pháp như các dạng trên
* Ví dụ 7: Tìm giới hạn sau:
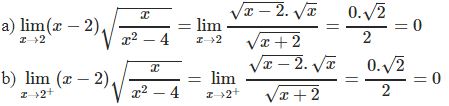
Bài tập vận dụng dạng 5
¤ Bài tập 1: Tìm các giới hạn sau
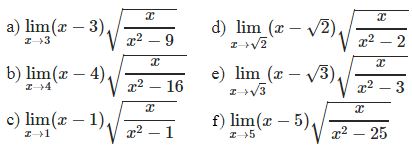
![]()
* Phương pháp: Ta cũng thường sử dụng các phương pháp như các dạng trên
* Ví dụ 8: Tìm giới hạn sau:
•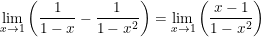
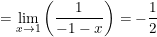
Bài tập vận dụng dạng 6:
¤ Bài tập 1: Tìm các giới hạn sau
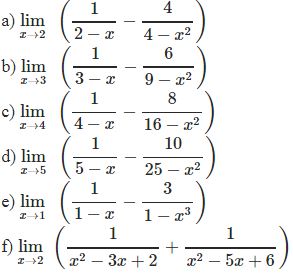
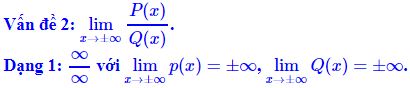
* Phương pháp:
_ Nếu P(x), Q(x) là các đa thức thì chia cả tử và mẫu cho luỹ thừa cao nhất của x
_ Nếu P(x), Q(x) có chứa căn thì có thể chia cả tử và mẫu cho luỹ thừa cao nhất của x hoặc nhân lượng liên hợp.

* Ví dụ 1: Tính các giới hạn sau
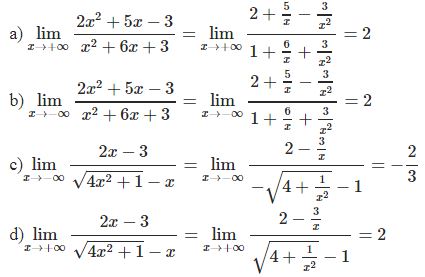
Bài tập vận dụng dạng 1:
¤ Bài tập 1: Tìm các giới hạn sau
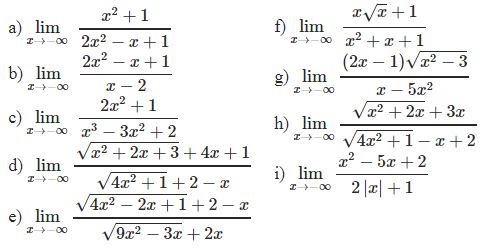
¤ Bài tập 2: Tìm các giới hạn sau
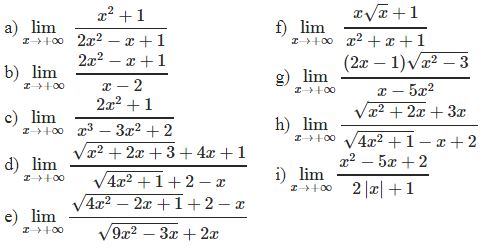

* Phương pháp: Ta thường sử dụng nhân lượng liên hợp cả tử và mẫu
* Ví dụ 2: Tìm các giới hạn
a)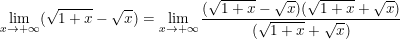
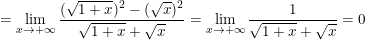
b)![small lim_{x
ightarrow -infty }(sqrt[3]{1+x^2-x^3}+x)](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941952564z6ge29jhr.gif)
![small =lim_{x
ightarrow -infty }frac{1+x^2}{left ( sqrt[3]{1+x^2-x^3}
ight )^2-xsqrt[3]{1+x^2-x^3}+x^2}](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/15941952574euypszvmx.gif)
![small =lim_{x
ightarrow -infty }frac{frac{1}{x^2}+1}{left ( sqrt[3]{frac{1}{x^3}+frac{1}{x}-1}
ight )^2-sqrt[3]{frac{1}{x^3}+frac{1}{x}-1}+1}=frac{1}{3}](https://hayhochoi.vn/uploads/news/wyswyg/2020_07/1594195259mxx47hbwo2.gif)
Bài tập vận dụng dạng 2:
¤ Bài tập 1: Tìm giới hạn sau
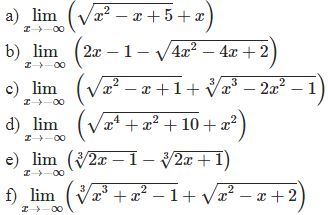
¤ Bài tập 2: Tìm giới hạn sau
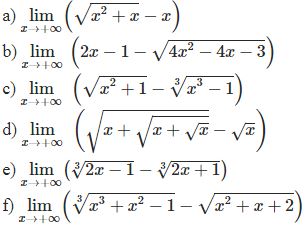

* Phương pháp: Sử dụng tổng hợp các phương pháp trên
* Ví dụ 3: Tìm các giới hạn sau:
a)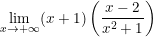
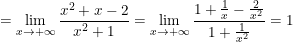
b)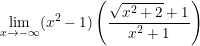
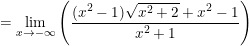
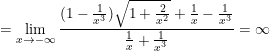
Do: 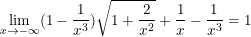 ;
; 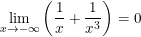
Bài tập vận dụng dạng 3:
¤ Bài tập 1: Tìm giới hạn sau
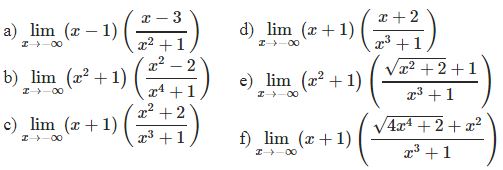
¤ Bài tập 2: Tìm các giới hạn sau
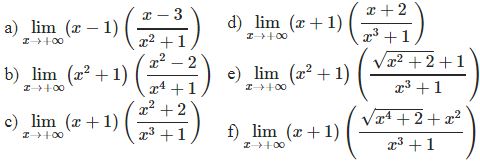
B. Mối quan hệ giữa giới hạn một bên và giới hạn tại một điểm
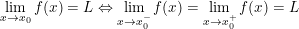
- Sử dụng cách tính giới hạn của hàm số.
* Ví dụ 1: Tìm giới hạn một bên của hàm số tại điểm được chỉ ra:
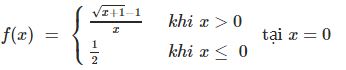
° Hướng dẫn:
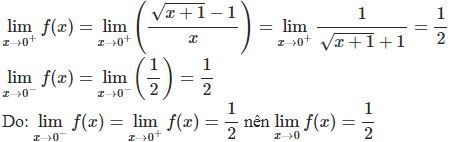
* Ví dụ 2: Tìm giá trị của m để các hàm số sau có giới hạn tại điểm được chỉ ra:
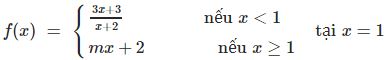
° Hướng dẫn:
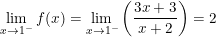
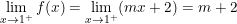
- Để hàm số có giới hạn tại x = 1 thì:
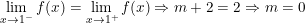
Bài tập vận dụng
¤ Bài tập 1: Tìm các giới hạn một bên của hàm số tại điểm được chỉ ra
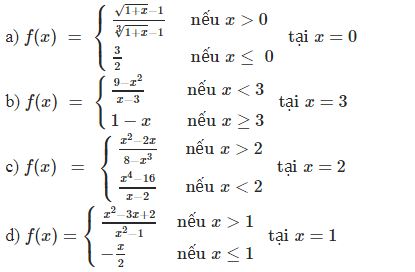
¤ Bài tập 2: Tìm giá trị của m để các hàm số sau có giới tại điểm được chỉ ra
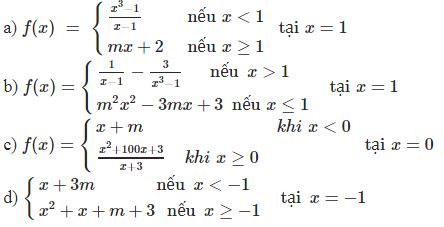
Hy vọng bài viết này đã giúp các em hiểu rõ hơn về các dạng toán giới hạn của hàm số. Nắm vững lý thuyết và các phương pháp giải là chìa khóa để các em tự tin giải quyết mọi bài tập. Hãy luyện tập thường xuyên để làm chủ kiến thức này nhé!
Đánh giá & nhận xét




















-
 Bài 7.27 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 7.27 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 6.17 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 6.17 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 9.12 trang 94 Toán 11 tập 2 Kết nối tri thức
Bài 9.12 trang 94 Toán 11 tập 2 Kết nối tri thức
-
 Bài 9.11 trang 94 Toán 11 tập 2 Kết nối tri thức
Bài 9.11 trang 94 Toán 11 tập 2 Kết nối tri thức
-
 Bài 9.10 trang 94 Toán 11 tập 2 Kết nối tri thức
Bài 9.10 trang 94 Toán 11 tập 2 Kết nối tri thức
-
 Bài 9.9 trang 94 Toán 11 tập 2 Kết nối tri thức
Bài 9.9 trang 94 Toán 11 tập 2 Kết nối tri thức
-
 Bài 9.8 trang 94 Toán 11 tập 2 Kết nối tri thức
Bài 9.8 trang 94 Toán 11 tập 2 Kết nối tri thức
-
 Bài 9.7 trang 94 Toán 11 tập 2 Kết nối tri thức
Bài 9.7 trang 94 Toán 11 tập 2 Kết nối tri thức
-
 Bài 9.6 trang 94 Toán 11 tập 2 Kết nối tri thức
Bài 9.6 trang 94 Toán 11 tập 2 Kết nối tri thức
-
 Bài 8.19 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.19 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.18 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.18 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.17 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.17 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.16 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.16 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.15 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.15 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.14 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.14 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.13 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.13 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.12 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.12 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.11 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.11 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 8.10 SGK Toán 11 Tập 2 Kết nối tri thức
Bài 8.10 SGK Toán 11 Tập 2 Kết nối tri thức
-
 Bài 12 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 12 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 11 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 11 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 10 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 10 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 9 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 9 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 8 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 8 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 7 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 7 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 6 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 6 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 5 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 5 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 4 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 4 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 3 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 3 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 2 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 2 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 1 trang 51 Toán 11 tập 2 Chân trời sáng tạo
Bài 1 trang 51 Toán 11 tập 2 Chân trời sáng tạo
-
 Bài 7.9 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.9 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.8 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.8 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.6 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.6 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức
Bài 7.5 trang 36 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.45 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.45 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.44 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.44 trang 65 Toán 11 tập 2 Kết nối tri thức
-
 Bài 7.43 trang 65 Toán 11 tập 2 Kết nối tri thức
Bài 7.43 trang 65 Toán 11 tập 2 Kết nối tri thức

















































