Bài 4.42 SGK Toán 11 tập 1 Kết nối tri thức

Đề bài 4.42 - SGK Toán 11 Tập 1 Kết nối tri thức:

Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, AA'.

a) Xác định giao điểm của mặt phẳng (MNP) với đường thẳng B'C.

b) Gọi K là giao điểm của mặt phẳng (MNP) với đường thẳng B'C. Tính tỉ số 

Hướng dẫn giải chi tiết bài 4.42 SGK Toán 11 Tập 1:

Ta có hình minh hoạ như sau:

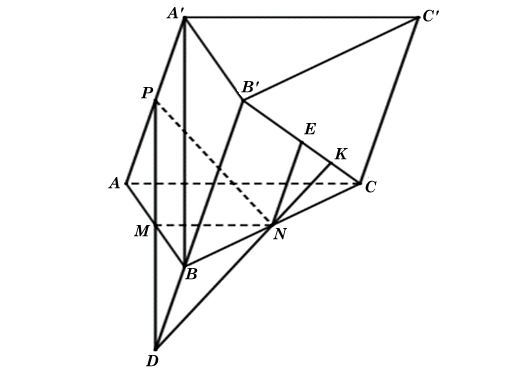
a) Trong mặt phẳng (ABB'A'), gọi D là giao điểm của PM và BB'.

Vì D thuộc BB' nên D thuộc mặt phẳng (BCC'B'), N thuộc BC nên N thuộc mặt phẳng (BCC'B'), do đó trong mặt phẳng (BCC'B') nối D với N, đường thẳng DN cắt B'C tại K.

Vì D thuộc PM nên D thuộc mặt phẳng (MNP), do đó DN nằm trong mặt phẳng (MNP).

Mà K thuộc DN nên K thuộc mặt phẳng (MNP).

Do vậy, K là giao điểm của mặt phẳng (MNP) với đường thẳng B'C.

b) Xét ΔA'AB có P, M lần lượt là trung điểm của các cạnh AA', AB nên PM là đường trung bình của Δ A'AB,

⇒ PM // A'B hay PD // A'B.

Lại có A'P // BD (vì AA' // BB' do nó là các cạnh bên của hình lăng trụ tam giác ABC.A'B'C').

⇒ Tứ giác A'PDB là hình bình hành.

⇒ A'P = BD.

Mà P là trung điểm của AA' nên A'P = AA', suy ra BD = AA'.

Lại có AA' = BB' (do ABC.A'B'C' là hình lăng trụ tam giác).

Từ đó suy ra BD = BB' (*)

 (**)

Gọi E là trung điểm của B'C. Vì N là trung điểm của BC, do đó EN là đường trung bình của tam giác BB'C, ⇒ EN // BB' và EN = BB' (***).

Từ (*) và (***) ⇒ EN = BD (****).

Từ (**) và (****) ⇒ 

Xét tam giác KDB' có EN // B'D (vì EN // BB'), theo định lí Thalés ta có:

⇒ KE = KB' ⇒ KE = EB'.

Mà EB' = EC (do E là trung điểm của B'C).

⇒ KE = KB' 

⇒ K là trung điểm của EC. Khi đó KC = EC

Mà EC = B'C.

Từ đó suy ra KC = KB'.

Vậy