Giải bài 4.39 trang 102 Toán 11 tập 1 SGK Kết nối tri thức

Bài 4.39 trang 102 Toán 11 tập 1 Kết nối tri thức:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SB, SD; K là giao điểm của mặt phẳng (AMN) và đường thẳng SC. Tỉ số  bằng

A. 1/2      B. 1/3

C. 1/4      D. 2/3

Giải bài 4.39 trang 102 Toán 11 tập 1 Kết nối tri thức:

* Đáp án: B

Ta có hình minh hoạ sau:

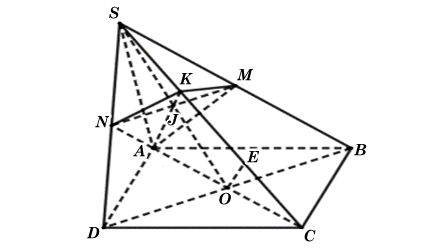
Gọi O là giao điểm hai đường chéo hình bình hành ABCD. Trong mặt phẳng (SBD), SO cắt MN tại J.

Trong mặt phẳng (SAC), AJ cắt SC tại K.

Vì J thuộc MN nên J thuộc mặt phẳng (AMN) nên K thuộc AJ thì K thuộc mặt phẳng (AMN). Do đó K là giao điểm của mặt phẳng (AMN) và đường thẳng SC.

Tam giác SBD có M, N lần lượt là trung điểm của các cạnh SB, SD nên MN là đường trung bình của tam giác SBD, suy ra MN // BD hay NJ // DO.

Xét ΔSDO có NJ // DO và N là trung điểm của SD nên suy ra J là trung điểm của SO.

Trong mặt phẳng (SAC), từ O kẻ OE song song với AK (E thuộc SC).

Xét ΔSOE có JK // OE (do AK // OE), theo định lí Thalés ta có: 

Xét ΔCAK có OE // AK, theo định lí Thalés ta có: 

Vì vậy, E là trung điểm của CK.

Vậy SK = KE = CE, suy ra