Bài 8 trang 84 Toán 8 Tập 2 Chân trời sáng tạo

Bài 8 trang 84 Toán 8 Tập 2 Chân trời sáng tạo: 

Cho hình thang ABCD (AB // CD), có hai đường chéo AC và BD cắt nhau tại O. Biết AB = 8 cm, CD = 20 cm. Khi đó ΔAOB ᔕ ΔCOD với tỉ số đồng dạng là

A. k = 2/3

B. k = 3/2

C. k = 2/5

D. k = 5/2

Phân Tích và Hướng Dẫn Giải:

1. Chứng minh Đồng dạng: Vì $AB // CD$, ta có các cặp góc so le trong bằng nhau ($\widehat{OAB} = \widehat{OCD}$ và $\widehat{OBA} = \widehat{ODC}$) và góc đối đỉnh ($\widehat{AOB} = \widehat{COD}$). Do đó, $\mathbf{\triangle AOB \backsim \triangle COD}$ theo trường hợp góc - góc (g.g).

2. Tỉ số Đồng dạng ($k$): Tỉ số đồng dạng $k$ là tỉ số của các cặp cạnh tương ứng:

   $k = \frac{AB}{CD} = \frac{OA}{OC} = \frac{OB}{OD}$

3. Tính $k$: Ta sử dụng hai cạnh đáy $AB$ và $CD$ để tính tỉ số.

Giải bài 8 trang 84 Toán 8 Tập 2 Chân trời sáng tạo: 

* Đáp án: C.

Ta có hình minh họa như sau:

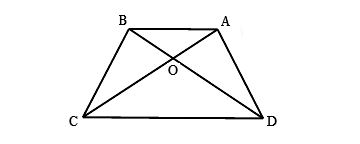
Ta có ΔAOB ᔕ ΔCOD với tỉ số đồng dạng: 

$k=\frac{AB}{CD}=\frac{8}{20}=\frac{2}{5}$