Bài 6 trang 66 Toán 8 Tập 2 Chân trời sáng tạo

Bài 6 trang 66 Toán 8 Tập 2 Chân trời sáng tạo: 

Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách BC ở hai địa điểm không thể đến được (Hình 15). Biết DE // BC.

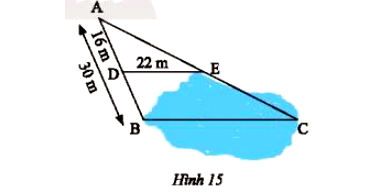
a) Chứng minh rằng ΔADE ᔕ ΔABC.

b) Tính khoảng cách BC.

Phân tích và Hướng Dẫn Giải

1. Chứng minh Đồng dạng (a): Sử dụng điều kiện $DE // BC$ để chứng minh $\triangle ADE \backsim \triangle ABC$ theo trường hợp Góc-Góc (g.g) (hoặc Hệ quả Định lý Thales).

2. Tính Khoảng cách (b):

   • Tính độ dài cạnh $AB = AD + DB$.

   • Thiết lập tỉ số đồng dạng: $\frac{AD}{AB} = \frac{DE}{BC}$.

   • Thay số và giải phương trình tìm $BC$.

Giải bài 6 trang 66 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Xét ΔABC có DE // BC nên ΔADE ᔕ ΔABC.

b) Vì ΔADE ᔕ ΔABC nên

$\frac{AD}{AB}=\frac{DE}{BC}\Leftrightarrow \frac{22}{BC}=\frac{16}{30}$

Suy ra: $BC=\frac{30.22}{16}=41,25\: (m)$

Vậy BC = 41,25 m.