Bài 3 trang 65 Toán 8 Tập 2 Chân trời sáng tạo

Bài 3 trang 65 Toán 8 Tập 2 Chân trời sáng tạo: 

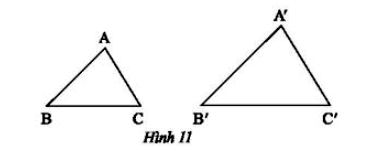
a) Trong Hình 11, cho biết ΔABC ᔕ ΔA′B′C′. Viết tỉ số đồng dạng của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

b) Trong Hình 12, cho biết ΔDEF ᔕ ΔD′E′F′. Tính số đo  và 

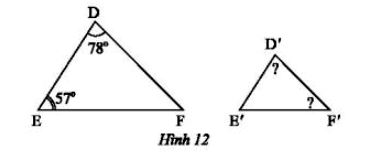
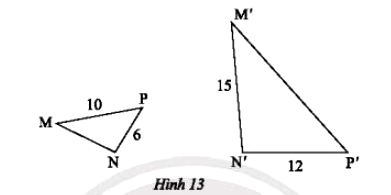
c) Trong Hình 13, cho biết ΔMNP ᔕ ΔM′N′P′. Tính độ dài các đoạn thẳng MN và M'P'.

Phân Tích Công thức và Tính chất

1. Tính chất cơ bản: Nếu $\triangle ABC \backsim \triangle A'B'C'$, thì:

   • Tỉ số cạnh: $\frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{AC}{A'C'}$.

   • Góc: $\widehat{A} = \widehat{A'}, \widehat{B} = \widehat{B'}, \widehat{C} = \widehat{C'}$.

2. Tổng ba góc: $\widehat{D} + \widehat{E} + \widehat{F} = 180^\circ$.

Giải bài 3 trang 65 Toán 8 Tập 2 Chân trời sáng tạo: 

a) ΔABC ᔕ ΔA′B′C′ nên ta có:

• $\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{AC}{A'C'}$

• $\widehat{A}=\widehat{A'};\: \widehat{B}=\widehat{B'};\: \widehat{C}=\widehat{C'}$

b) ΔDEF ᔕ ΔD′E′F′ nên ta có:

• $\widehat{D}=\widehat{D'}=78^o$

• $\widehat{F'}=\widehat{F}=180^o-(78^o+57^o)=45^o$

Vậy $\widehat{D'}=78^o;\: \: \widehat{F'}=45^o$

c) ΔMNP ᔕ ΔM′N′P′ nên ta có:

$\frac{MN}{M'N'}=\frac{NP}{N'P'}=\frac{MP}{M'P'}=\frac{1}{2}$

Suy ra $\frac{MN}{15}=\frac{6}{12}=\frac{10}{M'P'}=\frac{1}{2}$

Suy ra $MN=\frac{15}{2};\: \: M'P'=20$