Bài 3 trang 84 Toán 8 Tập 2 Chân trời sáng tạo: Định Lí Tam Giác Đồng Dạng

Đề bài 3 trang 84 Toán 8 Tập 2 CTST

Nếu tam giác ABC có MN // AB (với M ∈ AC, N ∈ BC) thì

A. ΔCMN ᔕ ΔABC.

B. ΔCNM ᔕ ΔCAB.

C. ΔCNM ᔕ ΔABC.

D. ΔMNC ᔕ ΔABC.

Phân tích và hướng dẫn giải:

Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo ra một tam giác mới đồng dạng với tam giác đã cho.

• Phân tích đề bài:

  • Tam giác ban đầu là $\Delta ABC$.

  • Đường thẳng $MN$ song song với cạnh $AB$.

  • Đường thẳng này cắt hai cạnh $AC$ tại $M$ và $BC$ tại $N$.

  • Tam giác mới được tạo thành là $\Delta MNC$.

Lời giải chi tiết bài 3 trang 84 Toán 8 CTST

* Đáp án: D.

Ta có hình minh họa như sau:

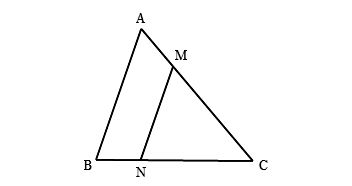
Theo định lí trên, khi có MN//AB, ta sẽ có tam giác $\Delta MNC$ đồng dạng với tam giác $\Delta ABC$. Tuy nhiên, việc sắp xếp thứ tự các đỉnh trong ký hiệu đồng dạng là rất quan trọng, phải đảm bảo các đỉnh tương ứng.

• Đỉnh $M$ tương ứng với đỉnh $A$.

• Đỉnh $N$ tương ứng với đỉnh $B$.

• Đỉnh $C$ là đỉnh chung nên tương ứng với chính nó.

Vậy, ta có thể viết: $\Delta MNC\sim\Delta ABC$.

Đáp án đúng là D.