Giải bài 5.6 trang 109 Toán 11 tập 1 SGK Kết nối tri thức

Đề bài:

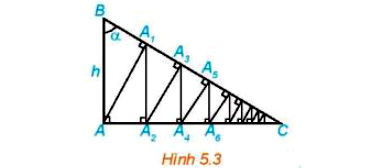
Cho tam giác vuông ABC vuông tại A, có AB = h và góc B bằng α (H.5.3). Từ A kẻ AA₁ ⊥ BC, từ A₁ kẻ A₁A₂ ⊥ AC, sau đó lại kẻ A₂A₃ ⊥ BC. Tiếp tục quá trình trên, ta được đường gấp khúc vô hạn AA₁A₂A₃... Tính độ dài đường gấp khúc này theo h và α.

Phân tích và Hướng dẫn giải:

Để giải bài toán này, ta cần thực hiện các bước sau:

1. Tính độ dài các đoạn thẳng đầu tiên: Sử dụng các hệ thức lượng trong tam giác vuông để tính độ dài các đoạn thẳng AA₁​,A₁​A₂​,A₂​A₃​,… theo $h$ và $\alpha$.

2. Xác định quy luật: Quan sát các kết quả đã tính để tìm ra quy luật của dãy độ dài các đoạn thẳng. Cụ thể, ta cần xác định xem chúng có tạo thành một cấp số nhân hay không.

3. Tính tổng: Nếu dãy độ dài tạo thành một cấp số nhân lùi vô hạn, ta sẽ sử dụng công thức tổng của nó để tính độ dài đường gấp khúc vô hạn.

Lời giải chi tiết:

• Tam giác AA₁B vuông tại A₁ có AB = h

Vì vậy: AA₁ = AB sinB = h.sinα.

Ta có:  và

• Tam giác AA₁A₂ vuông tại A₂ nên A₁A₂ = AA₁ sin = h.sinα.sinα = h.sin²α.

Vì AB ⊥ AC và A₁A₂ ⊥ AC nên AB // A₁A₂, suy ra  (2 góc đồng vị).

• Tam giác A₁A₂A₃ vuông tại A₃ nên A₂A₃ = A­₁A₂ . sin = h.sin²α.sinα = h.sin³α.

 Vì AA₁ ⊥ BC và A₂A₃ ⊥ BC nên AA₁ // A₂A₃, suy ra 

• Tam giác A₂A₃A₄ vuông tại A₄ nên A₃A₄ = A₂A₃ . sin = h.sin³α.sinα = h.sin⁴α.

Cứ tiếp tục như vậy, ta xác định được A_{n – 1}A_n = h.sinⁿα.

Ta có: AA₁A₂A₃... = AA₁ + A₁A₂ + A₂A₃ + ... + A_{n – 1}A_n + ...

= h sin α + h sin² α + h sin³ α + ... + h sinⁿ α + ...

Vì góc B là góc nhọn nên sin B = sin α < 1, do đó |sin α| < 1.

Khi đó, độ dài của đường gấp khúc vô hạn AA₁A₂A₃... là tổng của cấp số nhân lùi vô hạn với số hạng đầu u₁ = h sin α và công bội q = sin α.

Nên có: