Giải bài 1 trang 83 Toán 8 Tập 1 SGK Cánh Diều

Đề bài:

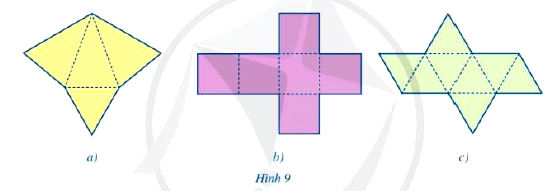
Trong các miếng bìa ở hình 9a, 9b, 9c, miếng bìa nào có thể gấp lại (theo các nét đứt) để được hình chóp tam giác đều?

Phân tích và Hướng dẫn giải:

Để xác định miếng bìa nào có thể gấp lại thành hình chóp tam giác đều, chúng ta cần nhớ lại cấu trúc của nó:

• Mặt đáy: Là một tam giác đều.

• Các mặt bên: Gồm ba tam giác cân bằng nhau.

• Tổng số mặt: Có 4 mặt (1 mặt đáy và 3 mặt bên).

Bây giờ, chúng ta sẽ lần lượt kiểm tra từng miếng bìa trong Hình 9:

• Hình 9a: Quan sát cấu tạo của miếng bìa này, ta thấy có một tam giác nằm ở giữa và ba tam giác khác nằm xung quanh. Các em cần kiểm tra xem tam giác ở giữa có phải là tam giác đều và ba tam giác xung quanh có phải là tam giác cân bằng nhau không.

• Hình 9b: Miếng bìa này có một hình vuông ở giữa và bốn tam giác xung quanh. Hình này không thể tạo thành hình chóp tam giác đều.

• Hình 9c: Miếng bìa này có một tam giác ở giữa và hai tam giác xung quanh. Số lượng mặt không đủ để tạo thành hình chóp.

Lời giải chi tiết:

Như ta đã biết: Hình chóp tam giác đều có 4 mặt, trong đó có 1 mặt đáy là tam giác đều và 3 mặt bên là các tam giác cân bằng nhau.

Từ quan sát hình 9 ta thấy trong tất cả các miếng bìa, chỉ có miếng bìa ở hình 9a thỏa mãn có 1 tam giác đều và 3 tam giác cân bằng nhau nên gấp được hình chóp tam giác đều.