Bài 2 trang 61 Toán 8 Tập 2 Cánh Diều

Bài 2 trang 61 Toán 8 Cánh Diều Tập 2:

Có thể gián tiếp đo chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không?

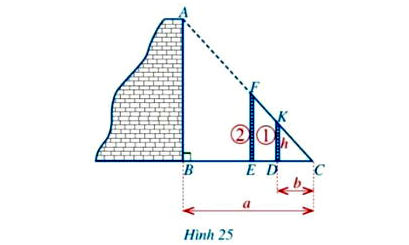
Hình 25 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: Hai cọc thẳng đứng (Cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao DK = h. Các khoảng cách BC=a, DC=b đo được bằng thước dây thông dụng.

a) Em hãy cho biết người ta tiến hành đo đạc như thế nào?

b) Tính chiều cao AB theo h, a, b.

Giải Bài 2 trang 61 Toán 8 Cánh Diều Tập 2:

a) Cách tiến hành:

- Đặt hai cọc thẳng đứng, vuông góc với mặt đất sau đó di chuyển cọc 2 sao cho 3 điểm A, F, K thẳng hàng.

- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).

Sử dụng định lý Ta – let để tính chiều cao AB.

b) Ta có:

$\left. \begin{array}{l}AB \bot AC\\DK \bot AB\end{array} \right\} \Rightarrow AB\parallel DK$

Xét tam giác ABC với AB//DK ta có:

$ \frac{{DK}}{{AB}} = \frac{{CD}}{{CB}}$ (Hệ quả của định lý Thales)

$ \Rightarrow AB = \frac{{DK.CB}}{{CD}} = \frac{{h.a}}{b}$