Bài 6 trang 73 Toán 8 Tập 2 Cánh Diều

Bài 6 trang 73 Toán 8 Cánh Diều Tập 2:

Cho hình bình hành ABCD. Một đường thẳng đi qua D lần lượt cắt đoạn thẳng BC và tia AB tại M và N sao cho điểm M nằm giữa hai điểm B và C. Chứng minh:

a) $\Delta NBM \backsim \Delta NAD$

b) $\Delta NBM \backsim \Delta DCM$

c)  $\Delta NAD \backsim \Delta DCM$

Phân Tích Hướng Dẫn Giải:

1. Tính chất Hình bình hành: $AD // BC$ và $AB // CD$.

2. Chứng minh (a) $\triangle NBM \sim \triangle NAD$ (g.g): Sử dụng $AD // BC$ (hay $AD // BM$) để tìm các cặp góc bằng nhau (góc chung, góc đồng vị hoặc so le trong).

3. Chứng minh (b) $\triangle NBM \sim \triangle DCM$ (g.g): Sử dụng $AB // CD$ (hay $NB // CD$) để tìm các cặp góc bằng nhau.

4. Chứng minh (c) $\triangle NAD \sim \triangle DCM$: Sử dụng tính chất bắc cầu của quan hệ đồng dạng.

Giải Bài 6 trang 73 Toán 8 Cánh Diều Tập 2:

Ta có hình vẽ sau:

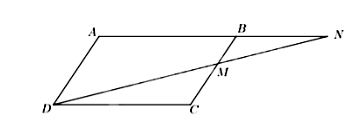
a) Vì ABCD là hình bình hành nên $AD//BC$ hay $AD//BM$

Suy ra $ \Delta NBM \backsim \Delta NAD$ (Định lý về cặp tam giác đồng dạng nhận dược từ định lý Thales)

b) Vì ABCD là hình bình hành nên $AB//CD$ hay $BN//CD$

Suy ra: $\Delta NBM \backsim \Delta DCM$ (Định lý về cặp tam giác đồng dạng nhận dược từ định lý Thales)

c) Ta có $ \Delta NBM \backsim \Delta NAD$ (chứng minh ở câu a)

và $\Delta NBM \backsim \Delta DCM$ (chứng minh ở câu b)

nên $\Delta NAD \backsim \Delta DCM$.