Bài 1 trang 60 Toán 8 Tập 2 Cánh Diều

Bài 1 trang 60 Toán 8 Cánh Diều Tập 2:

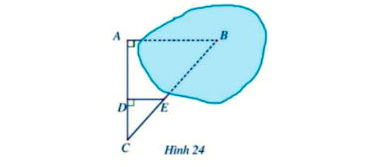
Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được, người ta tiến hành chọn các vị trí C, D, E như ở Hình 24 và đo được AC = 50m, CD = 20m, DE = 18m. 

Hỏi khoảng cách giữa hai vị trí A và B là bao nhiêu?

Phân Tích và Hướng Dẫn Giải:

1. Quan hệ Song song: Từ hình vẽ, ta thấy $AB \perp AC$ và $DE \perp AC$. Hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau: $\mathbf{AB // DE}$.

2. Định lý Thales: Vì $AB // DE$, ta áp dụng Định lý Thales (hoặc hệ quả) cho tam giác $ABC$.

3. Thiết lập Tỉ lệ thức: Tam giác $\triangle CDE$ và tam giác $\triangle CAB$ có $\widehat{C}$ chung và $DE // AB$ nên chúng đồng dạng ($\triangle CDE \sim \triangle CAB$).

   $\mathbf{\frac{DE}{AB} = \frac{CD}{CA}}$

4. Tính $AB$: Thay các giá trị đã biết vào tỉ lệ thức để tìm $AB$.

Giải Bài 1 trang 60 Toán 8 Cánh Diều Tập 2:

Ta có:

$ \left. \begin{array}{l}AB \bot AC\\DE \bot AC\end{array} \right\} \Rightarrow AB\parallel DE$

Xét tam giác ABC với AB//DE có: 

$ \frac{{DE}}{{AB}} = \frac{{CD}}{{CA}}$  (Hệ quả của định lý Thales) 

$\Rightarrow \frac{18}{AB} = \frac{20}{50}$

$\Rightarrow AB = 18.50:20$

AB = 45