Bài 8 trang 44 Toán 8 Tập 2 Cánh Diều

Bài 8 trang 44 Toán 8 Tập 2 Cánh Diều:

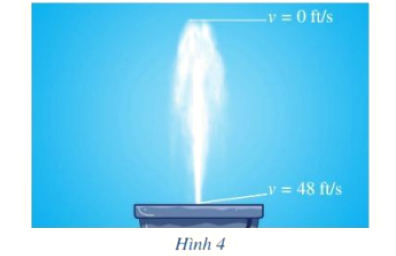
Hình 4 mô tả một đài phun nước. Tốc độ ban đầu của nước là 48 ft/s (ft là một đơn vị đo độ dài với 1 ft = 0,3048 m). Tốc độ v (ft/s) của nước tại thời điểm t (s) được cho bởi công thức: v = 48 – 32t. Tìm thời gian để nước đi từ mặt đài phun nước đến khi đạt được độ cao tối đa.

Phân Tích và Hướng Dẫn Giải

1. Xác định Điều kiện tại Độ cao Tối đa: Trong vật lý, khi một vật được ném thẳng đứng lên trên, tại điểm cao nhất (độ cao tối đa), vật sẽ dừng lại trong tích tắc trước khi rơi xuống. Do đó, tốc độ $v$ tại thời điểm này bằng 0.

2. Lập Phương trình: Thay $v = 0$ vào công thức tốc độ.

   $\mathbf{0 = 48 - 32t}$

3. Giải Phương trình: Giải phương trình bậc nhất để tìm $t$.

Giải bài 8 trang 44 Toán 8 Tập 2 Cánh Diều:

Khi xuất phát từ mặt đài phun nước, giọt nước có t = 0

Khi giọt nước đạt độ cao tối đa, v = 0. Thay vào công thức tính tốc độ ta có:

Khi nước đạt độ cao tối đa thì v = 0 ft/s.

Ta có phương trình:

48 – 32t = 0

–32t = –48

t = –48 : (–32)

t = 3/2 = 1,5 

Vậy thời gian cần để nước đi từ mặt đài phun nước đến khi đạt được độ cao tối đa là 1,5 (s).