Bài 4 trang 61 Toán 8 Tập 2 Cánh Diều

Bài 4 trang 61 Toán 8 Cánh Diều Tập 2:

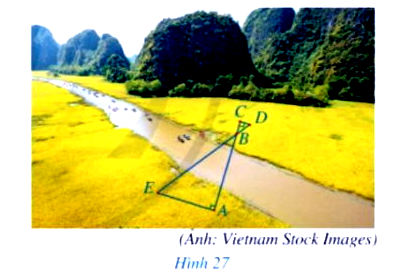
Anh Thiện và chị Lương đứng ở hai phía bờ song và muốn ước lượng khoảng cách giữa hai vị trí A, B ở hai bên bờ sông (Hình 27).

- Anh Thiện chọn vị trí C ở bên bờ sông sao cho A, B, C thẳng hàng và đo được BC=4m;

- Tiếp theo, anh Thiện xác định vị trí D, chị Lương xác định vị trí E sao cho D, B, E thẳng hàng, đồng thời $\widehat {BAE} = \widehat {BCD} = 90^\circ$;

- Anh Thiện đo được CD=2m, chị Lương đo được AE=12m.

- Hãy tính khoảng cách giữa hai vị trí A và B.

Phân Tích và Hướng Dẫn Giải:

1. Quan hệ Song song: Từ giả thiết $\widehat {BAE} = \widehat {BCD} = 90^\circ$, ta thấy $AE$ và $CD$ cùng vuông góc với đường thẳng $AC$ (hay đường thẳng chứa $AB$).

   $\Rightarrow \mathbf{AE // CD}$

2. Định lý Thales: Áp dụng Định lý Thales (hoặc tam giác đồng dạng) cho hai đường thẳng song song $AE$ và $CD$ cắt hai cát tuyến $AC$ và $DE$ tại điểm $B$.

3. Thiết lập Tỉ lệ thức: Tam giác $\triangle BAE$ và $\triangle BCD$ đồng dạng (hoặc $\triangle BCD \sim \triangle BAE$). 

    
   $\frac{AB}{BC} = \frac{AE}{CD}$

4. Tính $AB$: Thay các giá trị đã biết vào tỉ lệ thức.

Giải Bài 4 trang 61 Toán 8 Cánh Diều Tập 2:

Ta có:

$\left. \begin{array}{l}AE \bot AC\\CD \bot AC\end{array} \right\} \Rightarrow AE\parallel CD$

Xét tam giác ABE với AE//CD, ta có:

$\frac{{AB}}{{BC}} = \frac{{AE}}{{CD}}$ (Hệ quả của định lý Thales)

\Rightarrow \frac{{AB}}{4}$ $= \frac{{12}}{2} \Rightarrow AB = 12.4:2 = 24$

Vậy khoảng cách AB là 24m.