Giải bài 12 trang 121 Toán 8 Tập 1 SGK Cánh Diều: Hình thoi và hình bình hành

Đề bài:

Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:

a) OD = (1/2)CM và tam giác ACM là tam giác vuông;

b) Ba điểm A, D, M thẳng hàng;

c) Tam giác DCM là tam giác cân.

Phân tích và Hướng dẫn giải

Để chứng minh các yêu cầu của bài toán, ta sẽ sử dụng các tính chất sau:

• Hình thoi: Hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

• Hình bình hành: Các cặp cạnh đối song song và bằng nhau.

Ta sẽ lần lượt áp dụng các tính chất trên để chứng minh từng phần của bài toán.

Lời giải chi tiết bài 12 trang 121 Toán 8:

Ta có hình vẽ minh hoạ như sau: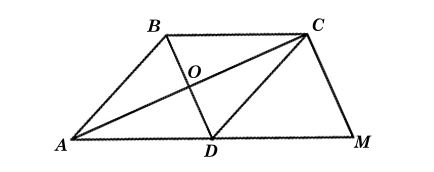

a) OD = (1/2)CM và tam giác ACM là tam giác vuông

• Vì ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Vì BCMD là hình bình hành nên BD = CM.

• Ta có: CM // BD (do BCMD là hình bình hành)

 AC ⊥ BD (chứng minh trên)

Do đó CM ⊥ AC hay 

Vây ΔACM là tam giác vuông (đpcm)

b) Ba điểm A, D, M thẳng hàng

Vì BCMD là hình bình hành nên DM // BC

Do đó qua điểm D có hai đường thẳng AD và DM cùng song song với đường thẳng BC nên AD trùng với DM (Tiên đề Euclid)

Hay ba điểm A, D, M thẳng hàng.

c) Tam giác DCM là tam giác cân

Theo chứng minh ở câu a) thì BD // CM nên ta có:

 (so le trong)   (*)

 (đồng vị)   (**)

Do ABCD là hình thoi nên DB là tia phân giác của góc ADC

Do đó:    (***)

Từ (*), (**) và (***) suy ra: 

⇒ Xét ΔDCM là tam giác cân tại D (đpcm)