Giải bài 5 trang 120 Toán 8 Tập 1 SGK Cánh Diều

Đề bài:

Hình 72 mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m. Tính khoảng cách từ điểm xa nhất của bóng cây đến đỉnh 4 m của cây.

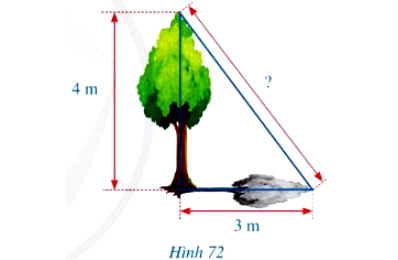
Phân tích và Hướng dẫn giải:

Để giải bài toán này, chúng ta cần mô hình hóa tình huống thực tế thành một mô hình hình học quen thuộc.

• Chiều cao của cây là một đoạn thẳng vuông góc với mặt đất.

• Bóng cây trên mặt đất là một đoạn thẳng nằm trên mặt đất.

• Khoảng cách từ điểm xa nhất của bóng cây đến đỉnh cây là một đoạn thẳng nối hai điểm đó.

Ba đoạn thẳng này tạo thành một tam giác vuông.

• Hai cạnh góc vuông lần lượt là chiều cao của cây và độ dài bóng cây.

• Cạnh huyền chính là khoảng cách cần tìm.

Để tìm độ dài cạnh huyền, chúng ta sẽ áp dụng định lý Pythagore: "Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông."

Công thức: c²=a²+b²

Lời giải chi tiết:

Giả sử Hình 72 được mô tả bởi tam giác ABC vuông tại A có các kích thước như hình sau:

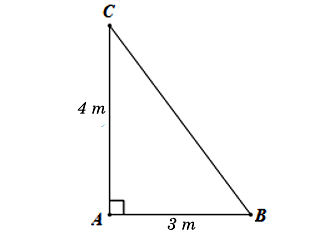Yêu cầu bài toán trở thành tìm độ dài cạnh BC.

Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 3² + 4² = 25

⇒ BC = 5 (m).

Vậy khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây là 5 m.