Giải bài 10 trang 121 Toán 8 Tập 1 SGK Cánh Diều

Đề bài:

Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm M, N, P, Q sao cho AM = BN = CP = DQ < AB. Chứng minh tứ giác MNPQ là hình vuông.

Phân tích và Hướng dẫn giải:

Để chứng minh tứ giác $MNPQ$ là hình vuông, chúng ta có thể sử dụng một trong các dấu hiệu nhận biết sau:

• Hình chữ nhật có hai cạnh kề bằng nhau.

• Hình chữ nhật có hai đường chéo vuông góc.

• Hình thoi có một góc vuông.

• Hình thoi có hai đường chéo bằng nhau.

Trong bài toán này, cách tiếp cận hiệu quả nhất là chứng minh tứ giác $MNPQ$ là hình thoi trước, sau đó chứng minh nó có một góc vuông.

Các bước giải sẽ là:

1. Chứng minh $MNPQ$ là hình thoi:

   • Sử dụng tính chất của hình vuông $ABCD$ và các giả thiết đã cho để chứng minh các tam giác vuông ở bốn góc ($AMQ$, $BNM$, $CPN$, $DQP$) bằng nhau.

   • Từ đó, suy ra bốn cạnh của tứ giác $MNPQ$ bằng nhau, và kết luận nó là hình thoi.

2. Chứng minh $MNPQ$ có một góc vuông:

   • Sử dụng các mối quan hệ về góc từ các tam giác vuông đã chứng minh ở bước trên.

   • Áp dụng tính chất tổng các góc trong tam giác vuông để suy ra một góc của tứ giác bằng 90∘.

3. Kết luận: Kết hợp hai kết quả trên để khẳng định $MNPQ$ là hình vuông.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

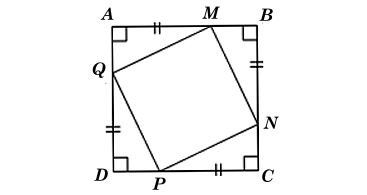
• Do ABCD là hình vuông nên AB = BC = CD = DA.

Mà AM = BN = CP = DQ

⇒ AB – AM = BC – BN = CD – CP = DA – DQ

Hay MB = NC = PD = QA

• Xét ΔAMQ và ΔBNM có:

AM = BN (giả thiết);

QA = MB (chứng minh trên)

Do đó ΔAMQ = ΔBNM (hai cạnh góc vuông)

Suy ra QM = MN (hai cạnh tương ứng).

Chứng minh tương tự ta có: MN = NP và NP = PQ.

Khi đó MN = NP = PQ = QM.

• Tứ giác MNPQ có 4 cạnh bằng nhau nên là hình thoi.

• Do ΔAMQ = ΔBNM (chứng minh trên) nên 

 (hai góc tương ứng)

Mà  (do ΔBMN vuông tại B)

Mặt khác: 

⇒ Hình thoi MNPQ có  nên là hình vuông.