Giải bài 5 trang 112 Toán 8 Tập 1 SGK Cánh Diều

Bài 5 trang 112 Toán 8 Tập 1 Cánh Diều:

Bạn Linh có một mảnh giấy dạng hình tròn. Bạn Linh đố bạn Bình: Làm thế nào có thể chọn ra 4 vị trí trên đường tròn đó để chúng là 4 đỉnh của một hình chữ nhật?

Bạn Bình đã làm như sau:

Bước 1. Gấp mảnh giấy sao cho hai nửa hình tròn trùng khít nhau. Nét gấp thẳng tạo thành đường kính của hình tròn. Ta đánh dấu hai đầu mút của đường kính đó là hai điểm A, C.

Bước 2. Sau đó lại gấp tương tự mảnh giấy đó nhưng theo đường kính mới và đánh dấu hai đầu mút của đường kính mới là hai điểm B, D. Khi đó tứ giác ABCD là hình chữ nhật (Hình 53).

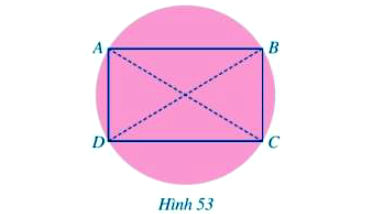
Em hãy giải thích cách làm của bạn Bình.

Giải bài 5 trang 112 Toán 8 Tập 1 Cánh Diều: 

Gọi O là giao điểm của hai đường kính AC và BD.

⇒ OA = OB = OC = OD (vì cùng bằng bán kính của hình tròn)

Tứ giác ABCD có hai đường chéo cắt nhau tại trung điểm O của mỗi đường nên là hình bình hành.

Mặt khác AC và BD là đường kính của hình tròn nên AC = BD

⇒ Hình bình hành ABCD có hai đường chéo AC, BD bằng nhau nên là hình chữ nhật.