Giải bài 2 trang 111 Toán 8 Tập 1 SGK Cánh Diều

Bài 2 trang 111 Toán 8 Tập 1 Cánh Diều:

Cho tam giác ABC vuông tại A có M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D cho MD = MA. Chứng minh tứ giác ABDC là sao hình chữ nhật và .

Giải bài 2 trang 111 Toán 8 Tập 1 Cánh Diều: 

Ta có hình minh hoạ như sau:

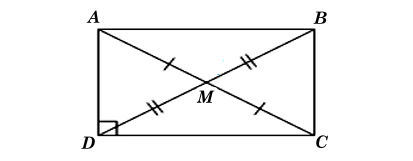
Theo bài ra, MD = MA nên M là trung điểm của AD.

Xét tứ giác ABDC có hai đường chéo AD và BC cắt nhau tại trung điểm M của mỗi đường

Vì vậy, ABDC là hình bình hành.

Mặt khác: 

Do đó hình bình hành ABDC là hình chữ nhật.

⇒ AD = BC.

Do M là trung điểm của AD nên có: 

 (đpcm)