Giải bài 5 trang 104 Toán 8 Tập 1 SGK Cánh Diều

Bài 5 trang 104 Toán 8 Tập 1 Cánh Diều:

Hình 33a là mặt cắt đứng phần chứa nước của một con mương (Hình 32) khi đầy nước có dạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC), H là hình chiếu của D trên đường thẳng AC.

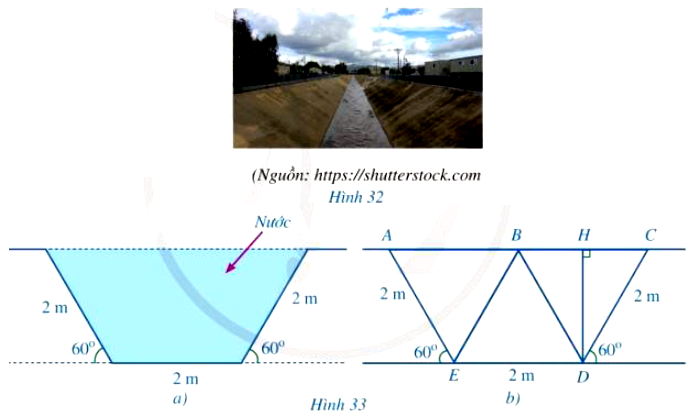
a) Chứng minh các tam giác BCD, BDE, ABE là các tam giác đều.

b) Tính độ dài của DH, AC.

c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước

Giải bài 5 trang 104 Toán 8 Tập 1 Cánh Diều:

Ta có hình minh hoạ như sau: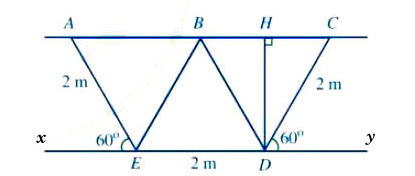

a) Chứng minh các tam giác BCD, BDE, ABE là các tam giác đều.

• Vì BD // AE nên 

và  (các cặp góc so le trong).

Ta có: 

ΔBCD có  nên là tam giác đều.

⇒ BD = BC = CD = 2 m.

• ΔBDE có BD = DE = 2 m nên là tam giác cân tại D

Mà   nên ΔBDE là tam giác đều.

⇒ BE = BD = DE =  2 m và 

• ΔABE có AE = BE = 2 m nên là tam giác cân tại E.

Vì AC // ED nên  (so le trong).

Nên ΔABE là tam giác đều.

b) Tính độ dài của DH, AC.

Do ΔBCD là tam giác đều nên đường cao BH đồng thời là đường trung tuyến của tam giác

Do đó H là trung điểm của BC nên:

Xét ΔDHC vuông tại H, theo định lí Pythagore có:

CD² = HC² + DH²

⇒ DH² = CD² – HC² = 2² – 1² = 3.

⇒ DH = √3 (m)

Vì ΔABE là tam giác đều nên AB = AE =  2 m.

Khi đó AC = AB + BC = 2 + 2 = 4 (m).

c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước là: