Giải bài 5 trang 97 Toán 8 Tập 1 SGK Cánh Diều

Bài 5 trang 97 Toán 8 Tập 1 SGK Cánh Diều:

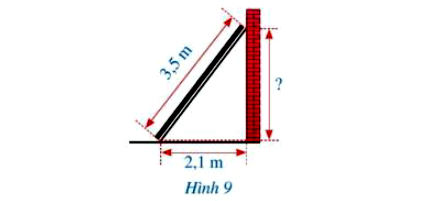
Hình 9 mô tả một thanh gỗ dài 3,5 m dựa vào một bức tường thẳng đứng. Chân thanh gỗ cách mép tường một khoảng là 2,1 m. Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là bao nhiêu mét?

Phân tích và Hướng dẫn giải:

Để giải bài toán này, chúng ta sẽ mô hình hóa tình huống thực tế thành một mô hình hình học quen thuộc. Thanh gỗ, bức tường và mặt đất tạo thành một tam giác vuông.

• Cạnh huyền chính là chiều dài của thanh gỗ.

• Một cạnh góc vuông là khoảng cách từ chân thanh gỗ đến tường.

• Cạnh góc vuông còn lại là khoảng cách từ điểm thanh gỗ chạm tường đến mặt đất, đây cũng là giá trị chúng ta cần tìm.

Để tìm độ dài cạnh góc vuông còn lại, ta sẽ áp dụng định lý Pythagore: "Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng bình phương của hai cạnh góc vuông."

Công thức: c²=a²+b²

Từ đó, ta có thể suy ra công thức tính cạnh góc vuông: a²=c²−b².

Lời giải chi tiết:

Vì bức tường vuông góc với mặt đất nên thanh gỗ dựa vào tường tạo thành một tam giác vuông ABC được mô tả như hình vẽ dưới đây.

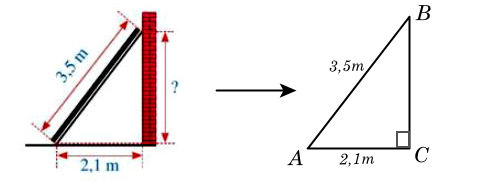
• Xét ΔABC vuông tại C, theo định lí Pythagore ta có:

AB² = AC² + BC²

⇒ BC² = AB² – AC² = 3,5² – 2,1² = 12,25 – 4,41 = 7,84 = 2,8²

⇒ BC = 2,8 m.

⇒ Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là 2,8 mét.