Giải bài 6 trang 97 Toán 8 Tập 1 SGK Cánh Diều

Đề bài 6 trang 97 Toán 8:

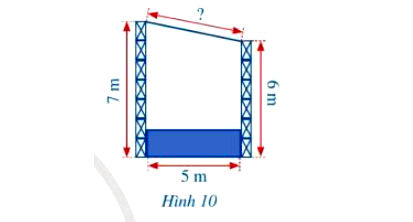
Hình 10 mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiều cao của khung phía trước khoảng 7 m, chiều cao của khung phía sau là 6 m, hai khung cách nhau một khoảng là 5 m. Chiều dài của mái che sân khấu đó là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?

Phân tích và Hướng dẫn giải

Để tính chiều dài của mái che sân khấu, chúng ta cần tìm độ dài của cạnh huyền của một tam giác vuông. Dựa vào hình mô tả, ta có thể tạo ra một tam giác vuông bằng cách kẻ một đường thẳng song song với mặt đất.

• Bước 1: Xác định các dữ kiện.

  • Chiều cao khung trước: 7 m.

  • Chiều cao khung sau: 6 m.

  • Khoảng cách giữa hai khung: 5 m.

• Bước 2: Tạo tam giác vuông.

  • Kẻ một đường thẳng từ đỉnh của khung sau (C) song song với mặt đất, cắt khung trước tại một điểm (A).

  • Ta có một tam giác vuông, với cạnh góc vuông là hiệu chiều cao của hai khung và khoảng cách giữa hai khung.

• Bước 3: Áp dụng định lý Pythagore.

  • Định lý Pythagore cho tam giác vuông với các cạnh góc vuông $a,b$ và cạnh huyền $c$ là: a²+b²=c².

• Bước 4: Tính toán và làm tròn.

  • Thay các giá trị đã biết vào công thức để tìm chiều dài mái che (cạnh huyền), sau đó làm tròn kết quả đến hàng phần trăm.

Lời giải chi tiết:

Mặt cắt đứng của sân khấu ngoài trời có mái che ở Hình 10 được mô tả như hình sau:

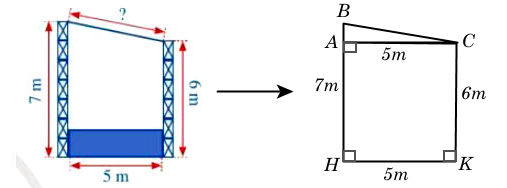Ta có: AB = BH – AH = BH – CK = 7 – 6 = 1 (m).

Xét tam giác ABC vuông tại A, theo định lí Pythagore ta có:

BC² = AB² + AC² = 1² + 5² = 1 + 25 = 26.

Vậy chiều dài của mái che sân khấu đó khoảng 5,1 mét.