Bài 7 trang 86 Toán 11 tập 2 Chân trời sáng tạo

Bài 7 trang 86 Toán 11 tập 2 Chân trời sáng tạo:

Nếu hình hộp chữ nhật có ba kích thước là 3, 4, 5 thì độ dài đường chéo của nó là

A. 5√2      B. 50.

C. 2√5      D. 12.

Phân Tích Hướng Dẫn Giải:

1. Định lý Pythagoras trong không gian: Đường chéo $d$ của hình hộp chữ nhật (nối hai đỉnh đối diện, ví dụ $A'$ và $C$) liên hệ với ba kích thước $a, b, c$ theo công thức tổng quát:

   $\mathbf{d = \sqrt{a^2 + b^2 + c^2}}$

2. Hoặc, Áp dụng tuần tự:

   • Bước 1: Tính đường chéo mặt đáy $AC = \sqrt{a^2 + b^2}$.

   • Bước 2: Tính đường chéo hình hộp $A'C = \sqrt{AC^2 + c^2}$.

Giải bài 7 trang 86 Toán 11 tập 2 Chân trời sáng tạo:

* Đáp án: A

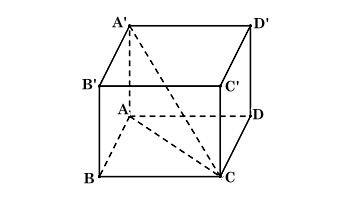
Giả sử hình hộp chữ nhật ABCD.A′B′C′D′ có AB = 3, BC = 4, AA′ = 5.

$AC=\sqrt{AB^2+BC^2}$ $=\sqrt{3^2+4^2}=5$

$A'C=\sqrt{AA'^2+AC^2}$ $=\sqrt{5^2+5^2}=5\sqrt{2}$