Bài 4 trang 86 Toán 11 tập 2 Chân trời sáng tạo

Bài 4 trang 86 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a và chiều cao bằng a√2. Khoảng cách từ tâm O của đáy ABC đến một mặt bên là

A. $\frac{a\sqrt{14}}{7}$     B. $\frac{a\sqrt{2}}{7}$

C. $\frac{a\sqrt{14}}{2}$    C.$\frac{2a\sqrt{14}}{7}$

Phân Tích Hướng Dẫn Giải:

1. Xác định hình chiếu: Hình chóp $S.ABC$ là hình chóp tam giác đều $\Rightarrow$ $SO$ là chiều cao, $O$ là trọng tâm tam giác đều $ABC$.

2. Mặt bên: Chọn mặt bên $(SBC)$.

3. Xác định khoảng cách:

   • Gọi $I$ là trung điểm $BC$. Ta có $BC \perp AI$ và $BC \perp SO$, suy ra $BC \perp (SAI)$.

   • Mặt phẳng $(SAI)$ là mặt phẳng vuông góc với cạnh chung $BC$ của mặt bên $(SBC)$ và mặt đáy $(ABC)$.

   • Trong mặt phẳng $(SAI)$, kẻ $OH \perp SI$ ($H \in SI$). Khi đó, $OH \perp (SBC)$.

   • Khoảng cách cần tìm là $d(O, (SBC)) = OH$.

4. Tính toán: Sử dụng hệ thức lượng trong tam giác vuông $SOI$ để tính $OH$.

Giải bài 4 trang 86 Toán 11 tập 2 Chân trời sáng tạo:

* Đáp án: A.

Ta có hình minh họa như sau:

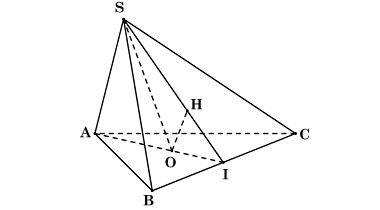
Gọi I là trung điểm của BC, kẻ OH ⊥ SI (H $\in$ SI).

Vì ΔABC là tam giác đều nên AI ⊥ BC

Ta có: SO⊥(ABC) nên SO⊥BC

⇒ BC ⊥ (SAI) ⇒ BC ⊥ OH

Mà OH ⊥ SI nên OH ⊥ (SBC)

Do đó d(O, (SBC)) = OH

ΔABC là tam giác đều nên:

$AI=a\sqrt{3}\Rightarrow OI=\frac{1}{3}AI=\frac{a\sqrt{3}}{3}$

ΔOHI vuông tại O, OH là đường cao:

$\frac{1}{OH^2}=\frac{1}{SO^2}+\frac{1}{OI^2}$

$=\frac{1}{(a\sqrt{2})^2}+\frac{1}{\left ( \frac{a\sqrt{3}}{3} \right )^2}$ $=\frac{1}{2a^2}+\frac{3}{a^2}=\frac{7}{2a^2}$

$\Rightarrow OH=\frac{a\sqrt{14}}{7}$