Bài 6 trang 56 Toán 11 tập 2 Chân trời sáng tạo

Bài 6 trang 56 Toán 11 tập 2 Chân trời sáng tạo:

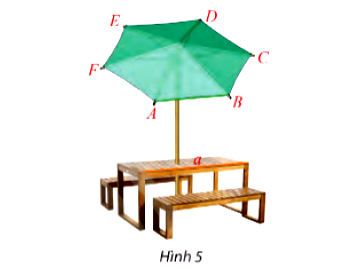
Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB song song với cạnh bàn a (Hình 5). Tính số đo góc hợp bởi đường thẳng a lần lượt với các đường thẳng AF, AE và AD.

Phân Tích Tính chất Lục giác Đều

Lục giác đều $ABCDEF$ có tâm $O$. Các tam giác $\triangle OAB, \triangle OBC, \dots$ đều là tam giác đều cạnh $R$ (với $R$ là độ dài cạnh lục giác). Các góc tại tâm của lục giác đều là $60^\circ$.

Quan trọng nhất, vì $AB // a$, nên góc giữa đường thẳng $a$ và một đường thẳng $XY$ bất kỳ sẽ bằng góc giữa $AB$ và $XY$:

Giải bài 6 trang 56 Toán 11 tập 2 Chân trời sáng tạo:

Ta có: AB // a, nên

(a, AF) = (AB, AF) = 120°

(a, AE) = (AB, AE) = 90°

(a, AD) = (AB, AD) = 60°