Bài 3 trang 56 Toán 11 tập 2 Chân trời sáng tạo

Bài 3 trang 56 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình chóp S.ABC có SA = SB = SC = a, $\widehat{BSA}=\widehat{CSA}=60^o$, $\widehat{BSC}=90^o$. Cho I và J lần lượt là trung điểm của SA và BC. Chứng minh rằng IJ ⊥ SA và IJ ⊥ BC.

Phân Tích và Hướng dẫn giải

1. Tam giác đều: $\triangle SAB$ có $SA=SB=a$ và $\widehat{BSA}=60^\circ$ $\Rightarrow \triangle SAB$ là tam giác đều cạnh $a$. Tương tự, $\triangle SAC$ cũng là tam giác đều cạnh $a$.

2. Chứng minh $IJ \perp SA$: Cần chứng minh $\triangle JSA$ hoặc $\triangle ISA$ cân tại $J$ hoặc $I$.

   • Ta sẽ chứng minh $\triangle JSA$ cân tại $J$, tức là $JA = JS$.

3. Chứng minh $IJ \perp BC$: Cần chứng minh $\triangle IBC$ hoặc $\triangle SBC$ cân tại $I$ hoặc $S$.

   • Ta sẽ chứng minh $\triangle IBC$ cân tại $I$, tức là $IB = IC$.

Giải bài 3 trang 56 Toán 11 tập 2 Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

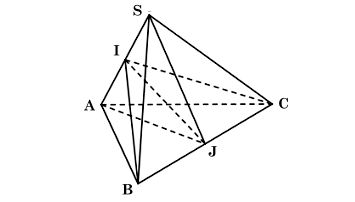
Xét tam giác SAB có:

SA = SB = a; $\widehat{BSA}=60^o$

⇒ Tam giác SAB đều.

Mà I là trung điểm của SA ⇒ IB = $\frac{a\sqrt{3}}{2}$

Xét tam giác SAC có:

SA = SC = a; $\widehat{ASC}=60^o$

⇒ Tam giác SAC đều.

Mà I là trung điểm của SA ⇒ IC = $\frac{a\sqrt{3}}{2}$

Ta có BSC là tam giác vuông cân tại S.

Suy ra: $BC=\sqrt{SB^2+SC^2}=a\sqrt{2}$

Xét tam giác ABC:

AB = AC = a

AB² + AC² = a² + a² = 2a²

$BC^2=\left ( a\sqrt{2} \right )^2=2a^2$

⇒ AB² + AC² = BC²

⇒ Tam giác ABC vuông cân tại A.

Mà J là trung điểm đoạn BC ⇒ AJ ⊥ BC

$\Rightarrow AJ=\sqrt{AB^2-BJ^2}$ $=\sqrt{a^2-\left ( \frac{a\sqrt{2}}{2} \right )^2}=\frac{a\sqrt{2}}{2}$

Xét tam giác SBC vuông cân tại S:

Mà J là trung điểm đoạn BC ⇒  SJ ⊥ BC

$\Rightarrow SJ=\sqrt{SB^2-BJ^2}$ $=\sqrt{a^2-\left ( \frac{a\sqrt{2}}{2} \right )^2}=\frac{a\sqrt{2}}{2}$

Xét tam giác JSA:

$AJ = SJ =\frac{a\sqrt{2}}{2}$

⇒  Tam giác JSA cân tại J.

Mà I là trung điểm của SA ⇒ IJ là đường trung tuyến của tam giác JSA.

hay IJ ⊥SA.

Xét tam giác IBC:

$IB = IC = \frac{a\sqrt{3}}{2}$

⇒ Tam giác IBC cân tại I.

Mà J là trung điểm của BC ⇒  IJ là đường trung tuyến của tam giác IBC.

hay IJ ⊥BC.