Hotline 0936685849

Bài 4 trang 56 Toán 11 tập 2 Chân trời sáng tạo: Góc Giữa Hai Đường Thẳng

10:49:3202/02/2024

Bài 4 trang 56 Toán 11 Tập 2 thuộc chương "Góc giữa hai đường thẳng và khoảng cách". Bài toán này giúp các em củng cố kiến thức về góc giữa hai đường thẳng trong hình học không gian, đặc biệt là trong tứ diện đều.

Đề bài

Cho tứ diện đều $A BC D$ cạnh $a$ . Gọi $K$ là trung điểm của $C D$ . Tính góc giữa hai đường thẳng $A K$ và $BC$ .

Phân tích kiến thức và hướng dẫn giải chi tiết

1. Phương pháp giải

Để tìm góc giữa hai đường thẳng chéo nhau $A K$ và $BC$ , ta có thể thực hiện một trong hai cách sau:

Cách 1: Phương pháp hình học
- Dựng một đường thẳng qua một điểm bất kỳ trên một trong hai đường thẳng và song song với đường thẳng còn lại.
- Góc giữa hai đường thẳng đã cho sẽ bằng góc giữa đường thẳng vừa dựng và đường thẳng còn lại.
Cách 2: Phương pháp vectơ
- Sử dụng công thức tính góc giữa hai vectơ: $\cos(\vec{u},\vec{v})=\frac{\vec{u}\cdot\vec{v}}{|\vec{u}|\cdot|\vec{v}|}$ .

Ở đây, ta sẽ sử dụng phương pháp hình học.

2. Lời giải chi tiết bài 4 trang 56 Toán 11

Ta có hình minh họa: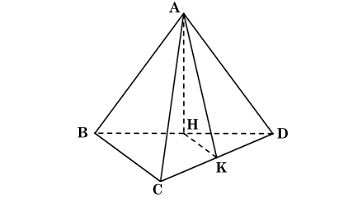

Bước 1: Tìm góc
- Gọi $H$ là trung điểm của $B D$ .
- Vì $K$ là trung điểm của $C D$ và $H$ là trung điểm của $B D$ , nên $HK$ là đường trung bình của tam giác $BC D$ .
- Suy ra $HK//BC$ và $HK=\frac{1}{2}BC=\frac{a}{2}$
- Góc giữa hai đường thẳng $A K$ và $BC$ chính là góc giữa $A K$ và $HK$ , tức là góc $A KH$ .
Bước 2: Tính độ dài các cạnh của tam giác $A HK$
- Tam giác $A B D$ là tam giác đều cạnh $a$ . Vì $H$ là trung điểm của $B D$ , nên $A H$ là đường cao, đồng thời là trung tuyến.
- $AH=\frac{a\sqrt{3}}{2}$ .
- Tương tự, tam giác $A C D$ là tam giác đều cạnh $a$ . Vì $K$ là trung điểm của $C D$ , nên $A K$ là đường cao.
- $AK=\frac{a\sqrt{3}}{2}$ .
- $HK=\frac{a}{2}$ (như đã tính ở trên).
Bước 3: Tính góc $\widehat{AKH}$
- Ta xét tam giác $A HK$ . Sử dụng định lí côsin:
  
  $AH^2=AK^2+HK^2-2\cdot AK\cdot HK\cdot\cos(\widehat{AKH})$
- Thay số vào:
  
  $(\frac{a\sqrt{3}}{2})^2=(\frac{a\sqrt{3}}{2})^2+(\frac{a}{2})^2-2\cdot(\frac{a\sqrt{3}}{2})\cdot(\frac{a}{2})\cdot\cos(\widehat{AKH})$
  
  $\frac{3a^2}{4}=\frac{3a^2}{4}+\frac{a^2}{4}-\frac{a^2\sqrt{3}}{2}\cos(\widehat{AKH})$
  
  $0=\frac{a^2}{4}-\frac{a^2\sqrt{3}}{2}\cos(\widehat{AKH})$
  
  $\frac{a^2\sqrt{3}}{2}\cos(\widehat{AKH})=\frac{a^2}{4}$
  $\cos(\widehat{AKH})=\frac{a^2/4}{a^2\sqrt{3}/2}=\frac{1}{2\sqrt{3}}=\frac{\sqrt{3}}{6}$
- $\widehat{AKH}=\arccos(\frac{\sqrt{3}}{6})\approx 73,2^\circ$

Tổng kết và lời khuyên

Đáp số:

Góc giữa hai đường thẳng $A K$ và $BC$ là $\approx 73,2^\circ$ .

Bài toán này là một ví dụ điển hình về việc sử dụng phương pháp hình học để giải bài toán trong không gian. Nắm vững các tính chất của đường trung bình và định lí côsin là chìa khóa để giải quyết bài toán một cách dễ dàng và chính xác. Chúc các em học tốt!

• Xem thêm Giải Toán 11 Tập 2 Chân trời sáng tạo SGK

> Bài 1 trang 56 Toán 11 tập 2 Chân trời sáng tạo: Cho hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a. Cho biết SA = a√3, SA ⊥ AB và SA ⊥ AD...

> Bài 2 trang 56 Toán 11 tập 2 Chân trời sáng tạo: Cho tứ diện đều ABCD. Chứng minh rằng AB ⊥ CD.

> Bài 3 trang 56 Toán 11 tập 2 Chân trời sáng tạo: Cho hình chóp S.ABC có SA = SB = SC = a, ∠BSA = ∠CSA = 60^o, ∠BSC = 90^o. Cho I và J lần lượt...

> Bài 4 trang 56 Toán 11 tập 2 Chân trời sáng tạo: Cho tứ diện đều ABCD cạnh a. Gọi K là trung điểm CD. Tính góc giữa hai đường thẳng AK và BC.

> Bài 5 trang 56 Toán 11 tập 2 Chân trời sáng tạo: Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của BC và AD. Biết AB = CD = 2a và MN = a√3...

> Bài 6 trang 56 Toán 11 tập 2 Chân trời sáng tạo: Một ô che nắng có viền khung hình lục giác đều ABCDEF song song với mặt bàn và có cạnh AB...