Bài 4 trang 85 Toán 11 tập 2 Chân trời sáng tạo

Bài 4 trang 85 Toán 11 tập 2 Chân trời sáng tạo:

Một con dốc có dạng hình lăng trụ đứng tam giác với kích thước như trong Hình 9.

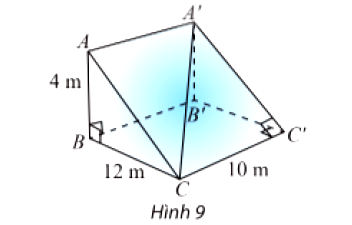
a) Tính số đo góc giữa đường thẳng CA′ và (CC′B′B).

b) Tính số đo góc nhị diện cạnh CC′.

Phân Tích Hướng Dẫn Giải:

1. Mô hình Lăng trụ đứng: Vì đây là lăng trụ đứng, ta có các cạnh bên vuông góc với mặt đáy ($\mathbf{A'A \perp (ABC)}$ và $\mathbf{CC' \perp (ABC)}$).

2. Góc $\angle(CA', (CC'B'B))$ (a):

   • Mặt phẳng $(CC'B'B)$ là mặt bên hình chữ nhật.

   • Ta cần tìm hình chiếu vuông góc của $A'$ lên mặt $(CC'B'B)$. Do lăng trụ đứng, $\triangle A'B'C'$ là đáy, $A'B'$ có vẻ là đường vuông góc hạ xuống $(CC'B'B)$ nếu $A'B' \perp C'B'$. (Tuy nhiên, theo hình vẽ, $A'B'C'$ là mặt đáy).

   • Xác định lại: $CA'$ là đường thẳng. $A'$ là hình chiếu của $A'$ lên $A'C'$. $\mathbf{A'B'}$ phải là đường vuông góc hạ từ $A'$ xuống mặt $(CC'B'B)$ nếu $A'B' \perp (CC'B'B)$. Điều này xảy ra nếu $A'B' \perp B'C'$ và $A'B' \perp C'C$. $A'B'$ vuông góc với $C'C$ là đúng (lăng trụ đứng). Nhưng $A'B' \perp B'C'$ (tức $\angle A'B'C' = 90^\circ$) chỉ xảy ra nếu $\triangle A'B'C'$ vuông tại $B'$. Giả sử $\triangle A'B'C'$ vuông tại $B'$ theo hình vẽ.

   • Khi đó, hình chiếu của $A'C$ lên $(CC'B'B)$ là $B'C$. Góc cần tìm là $\angle A'C B'$.

3. Góc nhị diện cạnh $CC'$ (b):

   • Giao tuyến là $CC'$.

   • Ta cần tìm hai đường thẳng cùng vuông góc với $CC'$ tại cùng một điểm, nằm trong $(A'C'C)$ và $(B'C'C)$. Vì $CC' \perp (A'B'C')$, ta có $\mathbf{C'A' \perp C'C}$ và $\mathbf{C'B' \perp C'C}$ (do $\angle A'C'B' = 90^\circ$). Góc phẳng nhị diện là $\angle A'C'B'$.

Giải bài 4 trang 85 Toán 11 tập 2 Chân trời sáng tạo:

a) Xét tam giác vuông CBB′ có: 

$B'C=\sqrt{BC^2+BB'^2}$ $=\sqrt{12^2+10^2}=\sqrt{244}=2\sqrt{61}\: (m)$

Gọi α là góc giữa đường thẳng (CA′, (CC′B′B)) = $\widehat{A'B'C}$

Khi đó: $tan\alpha =\frac{A'B'}{B'C}=\frac{4}{2\sqrt{61}}=\frac{2}{\sqrt{61}}$

Suy ra α ≈ 14^o22'

b) Ta có: CC′ ⊥ (ABC)

⇒ CC′ ⊥ AC, CC′ ⊥ BC.

Gọi β là góc phẳng nhị diện cạnh [A’, CC’, B’] = $\widehat{ACB}$

Khi đó: $tan\beta =\frac{A'B'}{B'C'}=\frac{4}{12}=\frac{1}{3}$

Suy ra: β ≈ 18^o26'