Bài 3 trang 81 Toán 11 tập 2 Chân trời sáng tạo

Bài 3 trang 81 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, $ SA = SB = SC = SD = a\sqrt{2}$. Gọi I, J lần lượt là trung điểm của AB và CD.

a) Chứng minh AB ⊥ (SIJ).

b) Tính khoảng cách giữa hai đường thẳng AB và SC.

Phân Tích Hướng Dẫn Giải:

1. Chứng minh $AB \perp (SIJ)$ (a): Chỉ cần chỉ ra $AB$ vuông góc với hai đường thẳng cắt nhau trong $(SIJ)$.

2. Tính $d(AB, SC)$ (b):

   • Nhận thấy $AB$ song song với $CD$, suy ra $AB$ song song với mặt phẳng $(SCD)$.

   • Khoảng cách $d(AB, SC) = d(AB, (SCD)) = d(I, (SCD))$.

   • Ta sẽ tính $d(O, (SCD))$ trước, sau đó suy ra $d(I, (SCD))$. Vì $O$ là trung điểm $IJ$, ta có $d(I, (SCD)) = d(J, (SCD))$ (do $IJ // CD \subset (SCD)$). Tuy nhiên, phương pháp được sử dụng trong lời giải gốc là dùng tỉ lệ khoảng cách qua $O$ và $I$ bằng cách kẻ $OK \perp SJ$ và $IH \perp SJ$.

Giải bài 3 trang 81 Toán 11 tập 2 Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

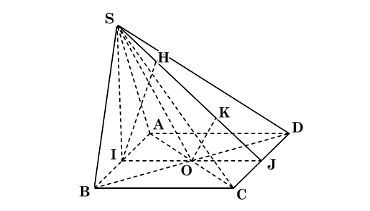
a) Ta có: ΔSAB cân tại S và đáy là hình vuông ABCD.

Nên SI ⊥ AB và IJ ⊥ AB

⇒ AB ⊥ (SIJ)

b) Ta có: AB // CD ⇒ AB // (ABCD)

⇒ d(AB, SC) = d(AB, (SCD)) = d(I, (SCD))

Gọi H, K lần lượt là hình chiếu vuông góc của I, O trên SJ

Ta có: IH // OK và IH = 2OK

Vì AB // CD nên CD ⊥ (SIJ) 

⇒ CD ⊥ IH 

⇒ IH ⊥ (SCD)

⇒ d(AB, CD) = d(AB, (SCD)) = IH = 2OK

Ta có: ABCD là hình vuông:

Suy ra: $OA=\frac{AC}{2}=\frac{\sqrt{AD^2+CD^2}}{2}$ $=\frac{\sqrt{a^2+a^2}}{2}=\frac{a\sqrt{2}}{2}$

• Xét ΔSAO vuông tại O có:

$SO=\sqrt{SA^2-OA^2}$ $=\sqrt{(a\sqrt{2})^2-\left ( \frac{a\sqrt{2}}{2} \right )^2}$ $=\frac{a\sqrt{6}}{2}$

• Xét ΔSOJ vuông tại O có đường cao OK nên

$OK=\frac{SO.OJ}{\sqrt{SO^2+OJ^2}}$ $=\frac{\frac{a\sqrt{6}}{2}.\frac{a}{2}}{\sqrt{\left ( \frac{a\sqrt{6}}{2} \right )^2+\left ( \frac{a}{2} \right )^2}}=\frac{a\sqrt{42}}{14}$

Vậy $d(AB, SC) = 2OK =\frac{a\sqrt{42}}{14}$