Bài 6 trang 82 Toán 11 tập 2 Chân trời sáng tạo

Bài 6 trang 82 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình hộp đứng ABCD.A′B′C′D′ có cạnh bên AA′ = 2a và đáy ABCD là hình thoi có AB = a và a

a) Tính khoảng cách giữa hai đường thẳng BD và AA′.

b) Tính thể tích của khối hộp.

Phân Tích Hướng Dẫn Giải:

1. Khoảng cách $d(BD, AA')$ (a): $AA'$ là cạnh bên, vuông góc với mặt đáy $(ABCD)$. $BD$ nằm trong mặt đáy. Khoảng cách giữa $BD$ và $AA'$ chính bằng khoảng cách từ $BD$ đến hình chiếu của $AA'$ trên mặt đáy.

   • Hình chiếu của $AA'$ lên $(ABCD)$ là điểm $A$.

   • Khoảng cách $d(BD, AA') = d(A, BD)$.

   • Trong hình thoi, $AC \perp BD$ tại $O$, nên $OA = d(A, BD)$.

2. Thể tích $V$ (b): Áp dụng công thức $V = h \cdot B$, với $h = AA'$ và $B = S_{ABCD}$. Diện tích hình thoi $S_{ABCD} = \frac{1}{2} AC \cdot BD$.

Giải bài 6 trang 82 Toán 11 tập 2 Chân trời sáng tạo:

Ta có hình minh hoạ như sau:

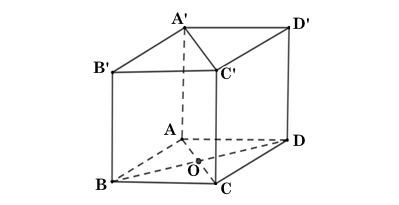
a) Vì hình hộp đứng ABCD.A'B'C'D' có đáy ABCD là hình thoi tâm O

Nên ta có: AA' ⊥ (ABCD) và AC ⊥ BD

Suy ra: AA' ⊥ OA và OA ⊥ BD

Vì vậy OA là đoạn vuông góc chung của hai đường thẳng BD và AA'

Vậy $d(BD, AA') = OA = AC/2$ $= \frac{a\sqrt{3}}{2}$

b) Vì đáy ABCD là hình thoi tâm O có AB = a và $AC = a\sqrt{3}$

Nên ta có: BD = 2OB 

$=2\sqrt{AB^2-OA^2}$ $=2\sqrt{a^2-\left ( \frac{a\sqrt{3}}{2} \right )^2}=a$

Thể tích của khối hộp là:

$V = AA'.S_ABCD=AA'.\frac{1}{2}AC.BD$ $=\frac{1}{2}.2a.a\sqrt{3}.a=a^3\sqrt{3}$

Vậy thể tích của khối hộp là $a^3\sqrt{3}$