Bài 3 trang 86 Toán 11 tập 2 Chân trời sáng tạo

Bài 3 trang 86 Toán 11 tập 2 Chân trời sáng tạo:

Cho hình chóp S.ABCD có các cạnh bên và cạnh đáy đều bằng a. Gọi M là trung điểm của SA. Mặt phẳng (MBD) vuông góc với mặt phẳng nào dưới đây?

A. (SBC).

B. (SAC).

C. (SBD).

D. (ABCD).

Phân Tích Hướng Dẫn Giải:

1. Xác định tính chất hình chóp: Hình chóp có tất cả các cạnh đều bằng nhau $S.ABCD$ là hình chóp đều. Đáy $ABCD$ là hình vuông.

2. Đường cao: Do các cạnh bên bằng nhau, chân đường cao $SO$ trùng với tâm $O$ của đáy (là giao điểm của $AC$ và $BD$). $SO \perp (ABCD)$.

3. Điều kiện vuông góc: Ta cần tìm một đường thẳng nằm trong $(MBD)$ vuông góc với một trong các mặt phẳng $A, B, C, D$.

4. Kiểm tra đường thẳng $BD$: $BD$ nằm trong mặt phẳng $(MBD)$. Ta sẽ kiểm tra xem $BD$ có vuông góc với mặt phẳng nào trong các lựa chọn hay không.

Giải bài 3 trang 86 Toán 11 tập 2 Chân trời sáng tạo:

* Đáp án: B

Ta có hình minh họa như sau:

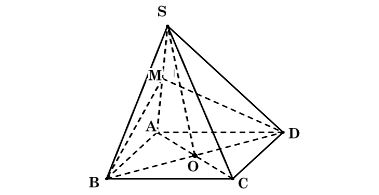
Gọi O là tâm của đáy.

Khi đó SO ⊥ (ABCD) nên SO ⊥ BD

Vì ABCD là hình vuông nên AC ⊥ BD.

Nên ta có: BD ⊥ (SAC) và BD ⊂ (MBD)

Suy ra: (MBD) ⊥ (SAC)