Hotline 0936685849

Bài 4 trang 93 Toán 11 tập 2 Chân trời sáng tạo: Sơ Đồ Hình Cây Xác Suất

18:11:4007/02/2024

Bài toán xác suất sử dụng sơ đồ hình cây là một dạng bài quen thuộc trong chương trình Toán 11. Bài viết này sẽ hướng dẫn các em giải Bài 4 trang 93 Toán 11 Tập 2 sách Chân Trời Sáng Tạo một cách chi tiết và dễ hiểu nhất.

Đề Bài:

Một xạ thủ bắn lần lượt 2 viên đạn vào một bia. Xác suất trúng đích của viên thứ nhất và thứ hai lần lượt là 0,9 và 0,6. Biết rằng kết quả các lần bắn độc lập với nhau. Tính xác suất của các biến cố sau bằng cách sử dụng sơ đồ hình cây:

a) “Cả 2 lần bắn đều trúng đích”;

b) “Cả 2 lần bắn đều không trúng đích”;

c) “Lần bắn thứ nhất trúng đích, lần bắn thứ hai không trúng đích”.

Phân Tích và Lời Giải:

Để giải bài toán này, trước hết chúng ta cần xác định xác suất của các biến cố cơ bản.

Gọi $A_{1}$ là biến cố "viên đạn thứ nhất trúng đích". Theo đề bài, ta có $P (A_{1}) = 0, 9$ .
Biến cố đối của $A_{1}$ là $\overline{A_1}$ : "viên đạn thứ nhất không trúng đích".

Xác suất của biến cố đối là $\overline{A_1}$ .
Gọi $A_{2}$ là biến cố "viên đạn thứ hai trúng đích". Ta có $P (A_{2}) = 0, 6$ .
Biến cố đối của $A_{2}$ là $\overline{A_2}$ : "viên đạn thứ hai không trúng đích".

Xác suất của biến cố đối là $\overline{A_2}$ .

Do hai lần bắn là độc lập, ta có thể biểu diễn tất cả các trường hợp có thể xảy ra và xác suất tương ứng bằng sơ đồ hình cây.

Ta có sơ đồ hình cây sau:

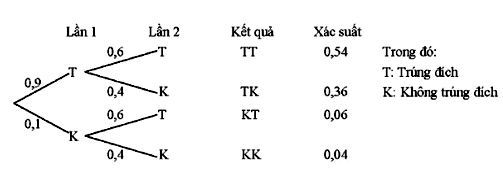
Giải bài 4 trang 93 Toán 11 tập 2 Chân trời sáng tạo

Gốc cây: "Bắn lần 1"
Nhánh 1: "Trúng" ( $A_{1}$ ) với xác suất $0, 9$
Nhánh 2: "Trượt" ( $\overline{A_1}$ ) với xác suất $0, 1$
Từ mỗi nhánh trên, vẽ tiếp nhánh con cho "Bắn lần 2":
- Từ nhánh $A_{1}$ :
  - Nhánh con 1: "Trúng" ( $A_{2}$ ) với xác suất $0, 6$
  - Nhánh con 2: "Trượt" ( $\overline{A_2}$ ) với xác suất $0, 4$
- Từ nhánh $\overline{A_1}$ :
  - Nhánh con 1: "Trúng" ( $A_{2}$ ) với xác suất $0, 6$
  - Nhánh con 2: "Trượt" ( $\overline{A_2}$ ) với xác suất $0, 4$ )

Từ sơ đồ hình cây, ta tính xác suất cho từng biến cố:

a) “Cả $2$ lần bắn đều trúng đích” Đây là biến cố giao $A_{1} \cap A_{2}$ . Áp dụng công thức nhân xác suất cho hai biến cố độc lập, ta có:

$P (A_{1} \cap A_{2}) = P (A_{1}) \cdot P (A_{2}) = 0, 9 \cdot 0, 6 = 0, 54$ .

b) “Cả $2$ lần bắn đều không trúng đích” Đây là biến cố giao $\overline{A_1}\cap\overline{A_2}$ .

$\overline{A_1}\cap\overline{A_2}$ .

c) “Lần bắn thứ nhất trúng đích, lần bắn thứ hai không trúng đích” Đây là biến cố giao $A_1\cap\overline{A_2}$ . $A_1\cap\overline{A_2}$ .

Sơ đồ hình cây là một công cụ trực quan mạnh mẽ giúp chúng ta dễ dàng hình dung và tính toán xác suất của các biến cố phức hợp, đặc biệt khi các biến cố là độc lập. Nắm vững phương pháp này sẽ giúp các em giải quyết nhiều dạng bài tập xác suất một cách hiệu quả. Chúc các em học tốt và đạt kết quả cao trong môn Toán!

Bài 4 trang 93 Toán 11 tập 2 Chân trời sáng tạo: Sơ Đồ Hình Cây Xác Suất

Đề Bài:

Phân Tích và Lời Giải:

Đánh giá & nhận xét