Giải bài 7 trang 121 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm các cạnh SA, SB. Chứng minh rằng:

a) MN // (SCD);

b) DM // (SBC);

c) Lấy điểm I thuộc cạnh SD sao cho  . Chứng minh rằng: SB // (AIC).

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, bạn cần nắm vững các định lý sau:

• Định lý đường trung bình trong tam giác: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng một nửa cạnh đó.

• Dấu hiệu nhận biết đường thẳng song song với mặt phẳng: Nếu một đường thẳng không nằm trong mặt phẳng và song song với một đường thẳng nào đó thuộc mặt phẳng đó, thì đường thẳng đó song song với mặt phẳng.

• Định lý Thales đảo: Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh đó các đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.

Áp dụng các định lý này, chúng ta sẽ lần lượt giải quyết từng phần của bài toán.

Lời giải chi tiết:

a) chứng minh MN // (SCD)

Ta có hình minh hoạ như sau: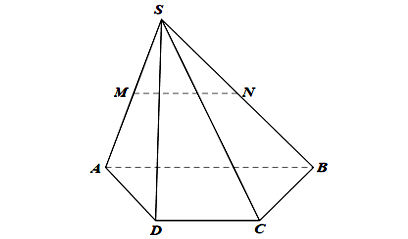

Trong mp(SAB), xét DSAB có M, N lần lượt là trung điểm của SA, SB nên MN là đường trung bình của tam giác

Do đó MN // AB.

Mà AB // CD (giả thiết) nên MN // CD.

Lại có CD ⊂ (SCD) ⇒ MN // (SCD).

b) chứng minh DM // (SBC)

Ta có hình minh hoạ như sau: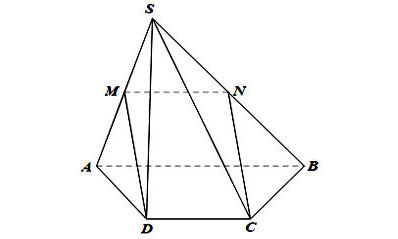

Theo câu a) thì MN là đường trung bình của ΔSAB nên MN = AB/2

Mà AB = 2CD hay CD = AB/2

⇒ MN = CD.

Xét tứ giác MNCD có: MN // CD và MN = CD nên MNCD là hình bình hành

⇒ DM // CN

Mà CN ⊂ (SBC) ⇒ DM // (SBC).

c) Chứng minh rằng: SB // (AIC)

Ta có hình minh hoạ như sau: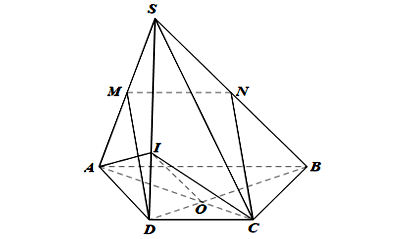

Trong mp(ABCD), gọi O là giao điểm của AC và BD.

Do AB // CD, theo hệ quả định lí Thalès ta có:

 Suy ra: 

• Trong mp(SDB), xét ΔSDB có 

Nên IO // SB (theo định lí Thalès đảo)

Mà IO ⊂ (AIC) ⇒ SB // (AIC).