Giải bài 6 trang 120 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh BC, SD. Xác định giao tuyến của mặt phẳng (AMN) với mỗi mặt phẳng sau:

a) (SCD)

b) (SBC).

Phân tích và Hướng dẫn giải

Để tìm giao tuyến của hai mặt phẳng, chúng ta cần tìm hai điểm chung của chúng. Đường thẳng đi qua hai điểm chung đó chính là giao tuyến cần tìm.

Trong bài toán này, để tìm giao tuyến của mặt phẳng $(AMN)$ với các mặt phẳng $(SCD)$ và $(SBC)$, chúng ta sẽ thực hiện các bước sau:

• Phần a:

  1. Tìm một điểm chung đã có sẵn.

  2. Tìm điểm chung thứ hai bằng cách kéo dài các đường thẳng trong các mặt phẳng. Cụ thể, ta sẽ kéo dài $AM$ trong mặt phẳng đáy để nó cắt một cạnh của mặt phẳng $(SCD)$.

• Phần b:

  1. Tìm một điểm chung đã có sẵn.

  2. Sử dụng giao tuyến vừa tìm được ở phần a. Giao tuyến này sẽ cắt một cạnh của mặt phẳng $(SBC)$, tạo ra điểm chung thứ hai.

Lời giải chi tiết:

a) Xác định giao tuyến của mặt phẳng (AMN) với (SCD)

Ta có hình minh hoạ như sau: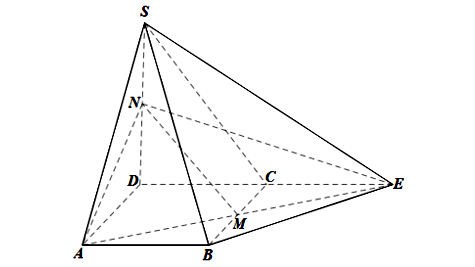

Trong mp(ABCD), kéo dài AM cắt DC tại E. Nối SE, BE.

Ta có: E ∈ AM mà AM ⊂ (AMN) nên E ∈ (AMN);

 E ∈ DC mà DC ⊂ (SCD) nên E ∈ (SCD).

Do đó E là giao điểm của hai mặt phẳng (AMN) và (SCD).

Lại có: N ∈ SD và SD ⊂ (SCD) nên N ∈ (SCD).

Mà N ∈ (AMN), nên N cũng là giao điểm của hai mặt phẳng (AMN) và (SCD).

⇒ (AMN) ∩ (SCD) = NE.

b) Xác định giao tuyến của mặt phẳng (AMN) với (SBC)

Ta có hình minh hoạ như sau:

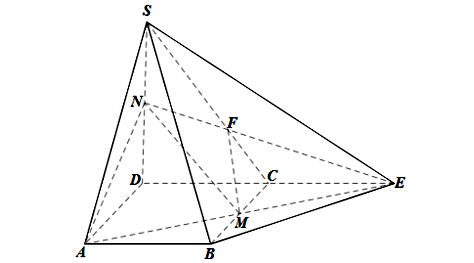
Trong mp(SCD), gọi F là giao điểm của SC và NE.

Ta có: F ∈ NE mà NE ⊂ (AMN) nên F ∈ (AMN);

 F ∈ SC mà SC ⊂ (SBC) nên F ∈ (SBC).

Do đó F là giao điểm của (AMN) và (SBC).

Lại có: M ∈ BC và BC ⊂ (SBC) nên M ∈ (SBC).

Mà M ∈ (AMN), nên M cũng là giao điểm của hai mặt phẳng (AMN) và (SBC).

⇒ (AMN) ∩ (SBC) = MF.