Giải bài 7 trang 100 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của các cạnh BC, CD. Trên cạnh AC lấy điểm K. Gọi M là giao điểm của BK và AI, N là giao điểm của DK và AJ. Chứng minh rằng đường thẳng MN song song với đường thẳng BD.

Phân tích và Hướng dẫn giải:

Để chứng minh $\mathbf{MN // BD}$, ta sẽ chứng minh rằng $MN$ và $BD$ là hai giao tuyến của hai cặp mặt phẳng song song với nhau (hoặc cùng song song với giao tuyến thứ ba).

1. Xác định giao tuyến $BD$: $BD$ là giao tuyến của mặt phẳng nào? Ta có thể chọn $\mathbf{(ABD)}$ và $\mathbf{(CBD)}$.

2. Xác định mặt phẳng chứa $MN$: $M \in (ABK), M \in (AIC)$. $N \in (ADK), N \in (AJC)$. Vậy $MN$ là giao tuyến của $\mathbf{(AIC)}$ và $\mathbf{(AJD)}$ (Lưu ý: $I$ không cùng mặt phẳng với $J$).

3. Cách tối ưu (Sử dụng định lí về giao tuyến song song):

   • Ta cần tìm hai mặt phẳng có giao tuyến $MN$ và $BD$. $\mathbf{BD}$ là cạnh, có thể xem là giao tuyến $\mathbf{(KBD) \cap (BCD)}$.

   • Mặt phẳng chứa MN: $M \in BK \subset (ABK)$, $N \in DK \subset (ADK)$. Ta chọn $\mathbf{(BKD)}$ và $\mathbf{(AIJ)}$.

   • Xác định 3 giao tuyến của 3 mặt phẳng:

     • $\mathbf{(BKD)} \cap \mathbf{(BCD)} = BD$

     • $\mathbf{(AIJ)} \cap \mathbf{(BCD)} = IJ$

     • $\mathbf{(BKD)} \cap \mathbf{(AIJ)} = MN$

   Nếu $IJ // BD$, thì theo định lí về giao tuyến song song, $MN // BD$.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

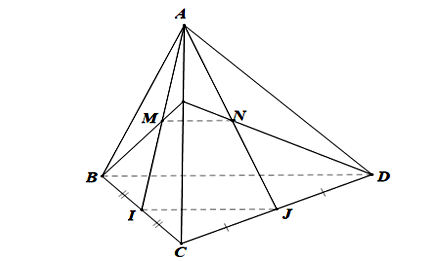
• Ta có: B ∈ (BDK) và B ∈ (BCD) nên B là giao điểm của (BDK) và (BCD).

D ∈ (BDK) và D ∈ (BCD) nên D là giao điểm của (BDK) và (BCD).

⇒ (BDK) ∩ (BCD) = BD.

• Ta có: M ∈ BK mà BK ⊂ (BDK) nên M ∈ (BDK); 

 M ∈ AI mà AI ⊂ (AIJ) nên M ∈ (AIIJ)

⇒ M là giao điểm của (BDK) và (AIJ)

Tương tự ta cũng có N là giao điểm của (BDK) và (AIJ)

⇒ (BDK) ∩ (AIJ) = MN.

• Ta có: I ∈ BC mà BC ⊂ (BCD) nên I ∈ (BCD)

Lại có I ∈ (AIJ) nên I là giao điểm của (BCD) và (AIJ)

Tương tự ta cũng có J là giao điểm của (BCD) và (AIJ)

⇒ (BCD) ∩ (AIJ) = IJ.

• Xét DBCD có I, J lần lượt là trung điểm của BC, CD nên IJ là đường trung bình của tam giác

⇒ IJ // BD.

• Ta có: (BDK) ∩ (BCD) = BD;

 (BDK) ∩ (AIJ) = MN;

 (BCD) ∩ (AIJ) = IJ;

 IJ // BD.

⇒ MN // BD.