Giải bài 7 trang 94 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Cho hình tứ diện ABCD. Gọi I là trung điểm cạnh CD. Gọi M, N lần lượt là trọng tâm các tam giác BCD, CDA.

a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI).

b) Gọi G là giao điểm của AM và BN. Chứng minh rằng: 

c) Gọi P, Q lần lượt là trọng tâm các tam giác DAB, ABC. Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và: 

Phân tích và Hướng dẫn giải:

1. Phần a: Sử dụng định nghĩa trọng tâm để chứng minh $M$ và $N$ nằm trên các trung tuyến $BI$ và $AI$, từ đó chúng thuộc $(ABI)$.

2. Phần b: Chứng minh $MN // AB$ bằng định lí Thalès đảo trong $\triangle ABI$, sau đó sử dụng hệ quả định lí Thalès trong $\triangle ABG$ để tìm tỉ số.

3. Phần c:

   • Đồng quy: Chứng minh $G$ cũng nằm trên $CP$ và $DQ$. Sử dụng sự đồng quy của $AM, BN$ tại $G$ và chứng minh $G$ là giao điểm chung của ba đường thẳng.

   • Tỉ số: Sử dụng tỉ lệ của trọng tâm và định lí Thalès để tìm tỉ số $\frac{GP}{GC}$ và $\frac{GQ}{GD}$.

Lời giải chi tiết:

a) Chứng minh rằng các điểm M, N thuộc mặt phẳng (ABI).

Ta có hình minh hoạ như sau:

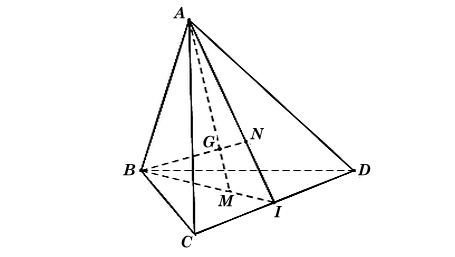
• Xét ΔBCD có: I là trung điểm của CD nên BI là đường trung tuyến.

Mà M là trọng tâm ΔBCD nên BI đi qua M.

⇒ M ∈ BI.

Lại có AI ⊂ (ABI) nên M ∈ (ABI).

• Xét ΔACD có: I là trung điểm của CD nên AI là đường trung tuyến.

Mà N là trọng tâm ΔACD nên AI đi qua N.

⇒ N ∈ AI.

Lại có BI ⊂ (ABI) nên N ∈ (ABI).

b) Chứng minh rằng: 

- Trong ΔBCD có M là trọng tâm tam giác nên: 

- Trong ΔACD có N là trọng tâm tam giác nên:

• Xét ΔABI có:  

⇒ MN // AB (theo định lí Thales đảo).

• Xét ΔABI và MN // AB theo hệ quả định lí Thales ta có:

• Xét ΔABG và MN // AB theo hệ quả định lí Thales ta có:

c) Chứng minh rằng các đường thẳng CP, DQ cùng đi qua điểm G và:  

Ta có hình minh hoạ như sau:

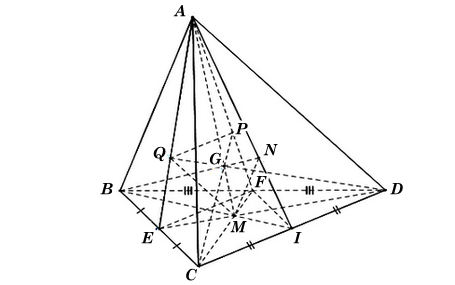• Gọi G’ là giao điểm của AM và CP;

• G’’ là giao điểm của AM và DQ.

Chứng minh tương tự câu b, ta có:

và:

Mà G, G’, G’’ cùng nằm trên AM nên G ≡ G’ ≡ G’’.

Vậy các đường thẳng CP, DQ cùng đi qua điểm G.

• Xét ΔABC, kẻ đường trung tuyến AE (E ∈ BC).

Ta có: Q là trọng tâm ΔABC nên 

• Xét ΔABD, kẻ đường trung tuyến AF (F ∈ BD).

Ta có: P là trọng tâm ΔABD nên

• Trong mặt phẳng (AEF), có:   nên PQ // EF (định lí Thales đảo)

Mà EF // CD (đường trung bình ΔBCD).

⇒ PQ // CD

- Theo hệ quả định lí Thales ta có: