Bài 1.8 Toán 12 tập 1 SGK Kết nối tri thức

Đề bài:

Cho hàm số y = f(x) = |x|

a) Tính các giới hạn  và 

Từ đó suy ra hàm số không có đạo hàm tại x = 0 

b) Sử dụng định nghĩa, chứng minh hàm số có cực tiểu tại x = 0 (xem hình 1.4)

Phương pháp giải:

Bài toán này có hai phần chính, đòi hỏi bạn phải sử dụng định nghĩa của đạo hàm và cực trị:

1. Tính giới hạn để xét đạo hàm: Một hàm số có đạo hàm tại một điểm \(x_0\) khi và chỉ khi giới hạn của tỉ số $$\frac{f(x) - f(x_0)}{x - x_0}$$ tại điểm đó tồn tại và hữu hạn. Nếu giới hạn trái và giới hạn phải không bằng nhau, hàm số không có đạo hàm tại \(x_0\).

2. Chứng minh cực tiểu bằng định nghĩa: Một hàm số \(f(x)\) đạt cực tiểu tại \(x_0\) nếu tồn tại một khoảng \((a; b)\) chứa \(x_0\) sao cho \(f(x) \ge f(x_0)\) với mọi \(x \in (a; b)\).

Lời giải chi tiết:

a) Ta có:

Vì  nên hàm số không có đạo hàm tại x = 0

b) Ta có:

Đồ thị hàm số y =|x|

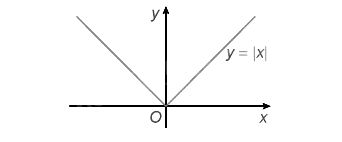
Hàm số y = f(x) = |x| liên tục và xác định trên (–∞; +∞)

Với h > 0 ta có: với x ∈ (-h; h) ⊂ (–∞; +∞) và x ≠ 0 thì y = f(x) = |x| > 0 = f(0)

Vì vậy, hàm số y = f(x) = |x| có cực tiểu là x = 0, y_CT = 0.