Bài 1.4 Toán 12 tập 1 SGK Kết nối tri thức

Đề bài:

Xét chiều biến thiên của các hàm số sau:

a) 

b) 

Phương pháp giải:

Để xét chiều biến thiên của một hàm số y = f(x), ta sử dụng phương pháp đạo hàm:

1. Tìm tập xác định D của hàm số. Đây là bước quan trọng đầu tiên, đặc biệt với các hàm có chứa căn.

2. Tính đạo hàm y' = f(x). Chú ý điều kiện để đạo hàm tồn tại.

3. Tìm các nghiệm của phương trình y'=0 và các điểm làm cho y' không xác định.

4. Lập bảng biến thiên: Dựa vào dấu của y' trên các khoảng, ta sẽ xác định được chiều biến thiên của hàm số.

Lời giải chi tiết:

a) 

TXĐ: D = [-2; 2]

Lập bảng biến thiên:

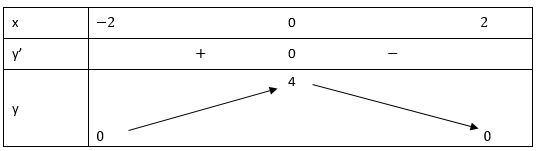
Vậy hàm số 

- Đồng biến trên khoảng (-2; 0)

- Nghịch biến trên khoảng (0; 2)

b) 

TXĐ: D = R

Lập bảng biến thiên:

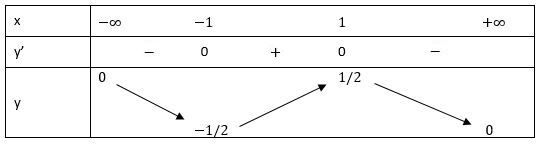
Vậy hàm số: 

- Đồng biến trên khoảng (-1; 1)

- Nghịch biến trên khoảng (-∞; -1) và (1; +∞)