Bài 3.3 trang 79 Toán 12 tập 1 Kết nối tri thức

Đề bài:

Bảng sau đây cho biết chiều cao của các học sinh lớp 12A và 12B.

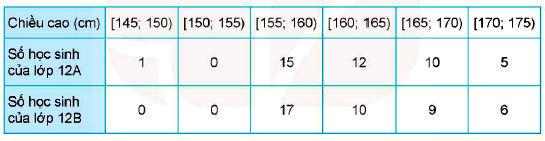
a) Tìm khoảng biến thiên, khoảng tứ phân vị cho các mẫu số liệu ghép nhóm về chiều cao của học sinh lớp 12A, 12B.

b) Để so sánh độ phân tán về chiều cao của học sinh hai lớp này ta nên dùng khoảng biến thiên hay khoảng tứ phân vị? Vì sao?

Phân tích và Hướng dẫn giải:

Bài toán này yêu cầu chúng ta tính toán các đại lượng thống kê cho dữ liệu ghép nhóm và đưa ra nhận xét dựa trên kết quả.

a) Tính khoảng biến thiên và khoảng tứ phân vị:

• Khoảng biến thiên (R): Đây là đại lượng đơn giản nhất, được tính bằng cách lấy cận trên của nhóm cuối cùng trừ đi cận dưới của nhóm đầu tiên. Công thức:

• $R = \text{max} - \text{min}$.

• Khoảng tứ phân vị (\(\Delta Q\)): Đây là một đại lượng phức tạp hơn, phản ánh sự phân tán của 50% dữ liệu ở giữa. Công thức: $\Delta Q = Q_3 - Q_1$. Để tính $Q_1$ và $Q_3$ cho dữ liệu ghép nhóm, ta sử dụng công thức nội suy tuyến tính:

  $Q_k = a + \frac{\frac{kN}{4} - n_a}{n_k} \cdot h$

  Với::

• $a$: Cận dưới của nhóm chứa $Q_k$

• $N$: Tổng số mẫu

• $n_a$: Tần số tích lũy của các nhóm trước nhóm chứa $Q_k$

• $n_k$: Tần số của nhóm chứa $Q_k$

• $h$: Chiều rộng của nhóm chứa $Q_k$

b) Lựa chọn đại lượng so sánh: Để so sánh độ phân tán, ta cần xem xét ưu và nhược điểm của cả hai đại lượng. Khoảng biến thiên dễ tính nhưng nhạy cảm với các giá trị bất thường (ngoại lai). Ngược lại, khoảng tứ phân vị chỉ tập trung vào phần trung tâm của dữ liệu, không bị ảnh hưởng bởi các giá trị quá lớn hoặc quá nhỏ.

Lời giải chi tiết:

Lớp 12A

+) Khoảng biến thiên: R₁ = 175 – 145 = 30.

+) Cỡ mẫu n = 1 + 0 + 15 + 12 + 10 + 5 = 43.

Gọi x₁; x₂; …; x₄₃ là chiều cao của 43 học sinh lớp 12A được sắp xếp theo thứ tự tăng dần.

Tứ phân vị thứ nhất của mẫu số liệu là x₁₁ thuộc nhóm [155; 160) nên nhóm chứa tứ phân vị thứ nhất là [155; 160).

Ta có $Q_1=155+\frac{\frac{43}{4}-1}{15}.(160-155)=158,25$

Tứ phân vị thứ ba của mẫu số liệu là x₃₃ thuộc nhóm [165; 170) nên nhóm chứa tứ phân vị thứ ba là [165; 170).

Ta có $Q_3=165+\frac{\frac{43.3}{4}-28}{10}.(170-165)=167,125$

Khoảng tứ phân vị là D_1Q = 167,125 – 158,25 = 8,875.

Lớp 12B

+) Khoảng biến thiên: R₂ = 175 – 155 = 20.

+) Cỡ mẫu n = 17 + 10 + 9 + 6 = 42.

Gọi y₁; y₂; …; y₄₂ là chiều cao của 42 học sinh lớp 12B và được sắp xếp theo thứ tự tăng dần.

Tứ phân vị thứ nhất của mẫu số liệu là y₁₁ thuộc nhóm [155; 160) nên nhóm chứa tứ phân vị thứ nhất là [155; 160).

Ta có $Q_1=155+\frac{\frac{42}{4}-0}{17}.(160-155)\approx 158,1$

Tứ phân vị thứ ba của mẫu số liệu là y₃₂ thuộc nhóm [165; 170) nên nhóm chứa tứ phân vị thứ ba là [165; 170).

Ta có $Q_2=165+\frac{\frac{42.3}{4}-27}{9}.(170-165)=167,5$

Khoảng tứ phân vị là: R_2Q = 167,5 – 158,1 = 9,4.

b) So sánh độ phân tán

Để so sánh độ phân tán về chiều cao của học sinh hai lớp, ta nên dùng khoảng tứ phân vị.

Lý do: Khoảng biến thiên ($R$) bị ảnh hưởng bởi các giá trị ở hai đầu của mẫu số liệu, bao gồm cả các giá trị bất thường (ngoại lai). Trong trường hợp này, dữ liệu của lớp 12A có một học sinh nằm ở nhóm $[145; 150)$, một giá trị rất nhỏ so với phần còn lại của lớp, làm cho khoảng biến thiên của lớp 12A ($R_A = 30$) lớn hơn đáng kể so với lớp 12B ($R_B = 20$).

Ngược lại, khoảng tứ phân vị ($\Delta Q$) chỉ tập trung vào 50% dữ liệu ở giữa, không bị ảnh hưởng bởi các giá trị bất thường ở hai đầu. Dựa vào khoảng tứ phân vị, ta thấy $\Delta Q_B = 9,41$ lớn hơn một chút so với $\Delta Q_A = 8,875$, cho thấy sự phân tán về chiều cao của học sinh lớp 12B lớn hơn. Điều này phản ánh chính xác hơn sự biến động về chiều cao của đa số học sinh trong mỗi lớp.