Bài 1.7 Toán 12 tập 1 SGK Kết nối tri thức

Đề bài:

Tìm cực trị của các hàm số sau:

a) y = 2x³ - 9x² + 12x - 5

b) y = x⁴ - 4x² + 2

c) 

d) 

Phương pháp giải:

Để tìm cực trị của một hàm số y = f(x), ta thực hiện các bước sau:

1. Tìm tập xác định D của hàm số. Đây là bước đầu tiên và quan trọng để xác định phạm vi xét.

2. Tính đạo hàm y'= f'(x).

3. Tìm các điểm tới hạn: Giải phương trình y' = 0 và tìm các điểm mà tại đó y' không xác định.

4. Lập bảng biến thiên hoặc sử dụng quy tắc đạo hàm bậc hai:

   • Bảng biến thiên: Xét dấu của y' trên các khoảng xác định. Nếu y' đổi dấu từ dương sang âm khi đi qua x₀, hàm số đạt cực đại tại x₀ (y_CĐ = f(x₀)). Nếu y' = 0 đổi dấu từ âm sang dương, hàm số đạt cực tiểu y_CT = f(x₀).

   • Quy tắc đạo hàm bậc hai: Nếu f'(x₀) = 0 và f''(x₀ ≠ 0):

     • Nếu \(f''(x_0) < 0\), hàm số đạt cực đại tại \(x_0\).

     • Nếu \(f''(x_0) > 0\), hàm số đạt cực tiểu tại \(x_0\) (ít dùng hơn).

Lời giải chi tiết:

a) y = 2x³ - 9x² + 12x - 5

TXĐ: D = R

y' = 6x² - 18x + 12 = 0 ⇔ x = 1 hoặc x = 2

Lập bảng biến thiên:

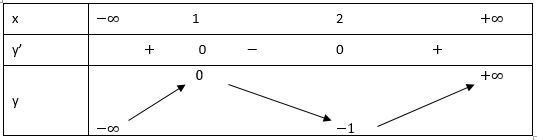
Vậy hàm số: y = 2x³ - 9x² + 12x - 5 có điểm cực đại là (1; 0) và điểm cực tiểu là (2; -1)

b) y = x⁴ - 4x² + 2

TXĐ: D = R

y' = 4x³ - 8x = 0 ⇔ x = 0 hoặc x = -√2 hoặc x = √2

Lập bảng biến thiên:

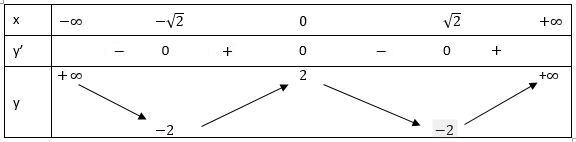
Từ bảng biến thiên, ta có:

Hàm số y = x⁴ - 4x² + 2 đạt cực đại tại x = 0 và y_CĐ = 2

Hàm số y = x⁴ - 4x² + 2 đạt cực tiểu tại  và y_CT = -2 

c) 

TXĐ: D = R\{1}

 (thỏa)

Lập bảng biến thiên:

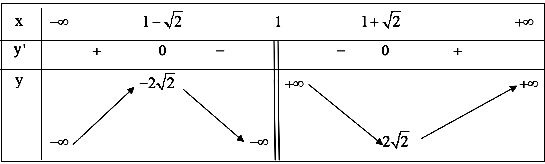
Từ bảng biến thiên ta có:

Hàm số  đạt cực đại tại  và 

Hàm số  đạt cực tiểu tại  và 

d) 

TXĐ: D = [0; 2]

⇔ x = 1 (thỏa)

Lâp bảng biến thiên:

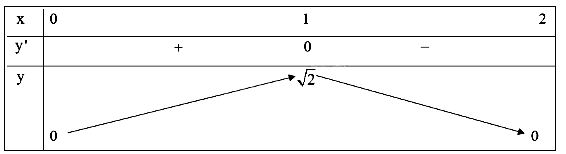
Từ bảng biến thiên, ta thấy:

Hàm số  đạt cực đại tại x = 1 và .

Hàm số  không có cực tiểu