Bài 1.6 Toán 12 tập 1 SGK Kết nối tri thức

Đề bài:

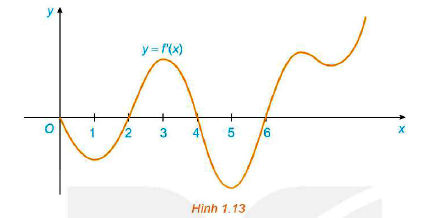
Đồ thị của đạo hàm bậc nhất y = f'(x) của hàm số f(x) được cho trong Hình 1.13:

a) Hàm số f(x) đồng biến trên những khoảng nào? Giải thích.

b) Tại giá trị nào của x thì f(x) có cực đại hoặc cực tiểu? Giải thích.

Phương pháp giải:

Để giải quyết bài toán này, bạn cần nhớ mối quan hệ giữa dấu của đạo hàm \(f'(x)\) và tính chất của hàm số \(f(x)\). Dựa vào đồ thị \(y = f'(x)\):

• Nếu đồ thị nằm phía trên trục hoành (tức là f'(x) > 0), hàm số f(x) đồng biến.

• Nếu đồ thị nằm phía dưới trục hoành (tức là \(f'(x) < 0\)), hàm số f(x) nghịch biến.

• Điểm cực trị của f(x) xảy ra tại các điểm x mà tại đó f'(x) = 0 (đồ thị cắt trục hoành) và f'(x) đổi dấu.

  • f'(x) đổi dấu từ âm sang dương (\(- \to +\)) thì f(x) có cực tiểu.

  • f'(x) đổi dấu từ dương sang âm (\(+ \to -\)) thì f(x) có cực đại.

Lời giải chi tiết:

a) Vì f'(x) > 0 khi x ∈ (2; 4) và x ∈ (6; +∞). 

Nên hàm số f(x) đồng biến trên (2; 4) và (6; +∞).

Vì f'(x) < 0 khi x ∈ (0; 2) và x ∈ (4; 6). 

Nên hàm số f(x) nghịch biến trên (0; 2) và (4; 6). 

b) Vì f'(x) < 0 với mọi x ∈ (0; 2) và f'(x) > 0 với mọi x ∈ (2; 4) thì x = 2 là một điểm cực tiểu của hàm số f(x).

Vì f'(x) > 0 với mọi x ∈ (2; 4) và f'(x) < 0 với mọi x ∈ (4; 6) thì điểm x = 4 là một điểm cực đại của hàm số f(x).

Vì f'(x) < 0 với mọi x ∈ (4; 6) và f'(x) > 0 với mọi x ∈ (6; +∞) thì x = 6 là một điểm cực tiểu của hàm số f(x).