Hotline0936685849

Bài 1.16 trang 25 Toán 12 tập 1 Kết nối tri thức: Giới Hạn & Tiệm Cận

16:56:53Cập nhật: 25/09/2025

Bài 1.16 trang 25 Toán 12 Tập 1 thuộc chương "Giới hạn". Bài tập này giúp các em củng cố kiến thức về cách đọc và phân tích đồ thị hàm số để xác định giới hạn tại vô cực và giới hạn tại một điểm, từ đó suy ra các đường tiệm cận của đồ thị hàm số.

Đề bài:

Hình 1.26 là đồ thị của hàm số $y=f(x)=\frac{2x^2}{x^2-1}$ . Sử dụng đồ thị này, hãy:

a) Viết kết quả của các giới hạn sau: $\lim_{x\to-\infty}f(x)$ ; $\lim_{x\to+\infty}f(x)$ ; $\lim_{x\to 1^-}f(x)$ ; $\lim_{x\to-1^+}f(x)$ .

b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.

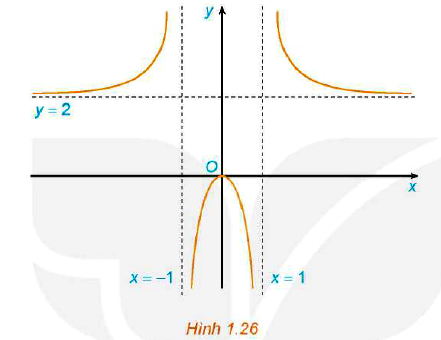
Bài 1.16 trang 20 Toán 12 Tập 1 Kết nối tri thức

Phân tích và hướng dẫn giải chi tiết

a) Viết kết quả của các giới hạn

Dựa vào đồ thị, ta có thể xác định các giới hạn:

Khi $x\to-\infty$ , đồ thị hàm số tiến dần đến đường thẳng $y=2$ . $\lim_{x\to-\infty}f(x)=2$
Khi $x\to+\infty$ , đồ thị hàm số cũng tiến dần đến đường thẳng $y=2$ . $\lim_{x\to+\infty}f(x)=2$
Khi $x\to 1^-$ (tiến về 1 từ phía trái), đồ thị hàm số có nhánh lao xuống vô cực âm. $\lim_{x\to 1^-}f(x)=-\infty$
Khi $x\to-1^+$ (tiến về -1 từ phía phải), đồ thị hàm số cũng có nhánh lao xuống vô cực âm. $\lim_{x\to-1^+}f(x)=-\infty$

b) Chỉ ra các tiệm cận

Tiệm cận ngang: Dựa vào kết quả giới hạn ở vô cực ( $\lim_{x\to\pm\infty}f(x)=2$ ), ta thấy đồ thị hàm số có một tiệm cận ngang là đường thẳng $y=2$ .
Tiệm cận đứng: Dựa vào kết quả giới hạn khi $x$ tiến về một giá trị hữu hạn mà kết quả là vô cực ( $\lim_{x\to 1^-}f(x)=-\infty$ và $\lim_{x\to-1^+}f(x)=-\infty$ ), ta thấy đồ thị hàm số có hai tiệm cận đứng là các đường thẳng $x=1$ và $x=-1$ .

Đáp số:

a) $\lim_{x\to-\infty}f(x)=2$ ; $\lim_{x\to+\infty}f(x)=2$ ; $\lim_{x\to 1^-}f(x)=-\infty$ ; $\lim_{x\to-1^+}f(x)=-\infty$ .

b) Đồ thị hàm số có tiệm cận ngang là đường thẳng y = 2, và hai tiệm cận đứng là các đường thẳng x = 1 và x = -1.

Bài toán này giúp các em làm quen với việc đọc các giới hạn từ đồ thị và xác định các đường tiệm cận tương ứng. Nắm vững mối liên hệ giữa giới hạn và tiệm cận là rất quan trọng trong giải tích. Chúc các em học tốt!

• Xem thêm:

Bài 1.17 trang 25 Toán 12 Tập 1 Kết nối tri thức: Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số y = (x² + 2x - 3)/(x - 1) không?...

Bài 1.18 trang 25 Toán 12 Tập 1 Kết nối tri thức: Tìm các tiệm cận của đồ thị hàm số sau: a) y = (3 - x)/(2x + 1)...

Bài 1.19 trang 25 Toán 12 Tập 1 Kết nối tri thức: Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là: C(x) = 2x + 50...

Bài 1.20 trang 25 Toán 12 Tập 1 Kết nối tri thức: Một mảnh vườn hình chữ nhật có diện tích 144 m². Biết độ dài của một cạnh mảnh vường là x (m)....