Giải bài 5 trang 104 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi M, N lần lượt là trọng tâm của hai tam giác ABF và ABC. Chứng minh rằng đường thẳng MN song song với mặt phẳng (ACF).

Phân tích và Hướng dẫn giải

Để chứng minh một đường thẳng song song với một mặt phẳng, chúng ta thường sử dụng phương pháp sau:

• Tìm một đường thẳng khác nằm trong mặt phẳng đó.

• Chứng minh rằng đường thẳng ban đầu song song với đường thẳng vừa tìm được.

Trong bài toán này, chúng ta cần chứng minh đường thẳng MN song song với mặt phẳng (ACF). Chúng ta sẽ tìm một đường thẳng nằm trong (ACF) và chứng minh MN song song với nó. Đường thẳng đó chính là FC.

• Bước 1: Xác định vị trí của các điểm M, N.

  • M là trọng tâm của Δ$ABF$.

  • N là trọng tâm của Δ$ABC$.

• Bước 2: Sử dụng tính chất của trọng tâm để tìm các tỉ lệ thức liên quan đến các đoạn thẳng.

• Bước 3: Áp dụng định lí Thales đảo để chứng minh MN song song với một đường thẳng nằm trong mặt phẳng (ACF).

Lời giải chi tiết bài 5 trang 104 Toán 11:

Ta có hình minh hoạ như sau:

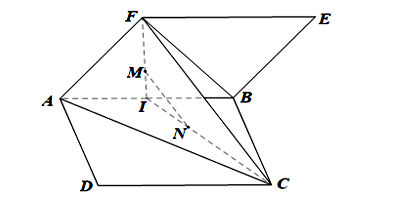
Gọi I là trung điểm của AB.

Xét DABF có M là trọng tâm của tam giác nên: 

Xét DABC có N là trọng tâm của tam giác nên:

Trong mặt phẳng ACF, xét ΔACF có: 

⇒ MN // FC (theo định lí Thalès)

Mà FC ⊂ (ACF).

Do đó MN // (ACF).