Giải bài 3 trang 100 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P lần lượt là trung điểm của các cạnh SA, AB, SD. Xác định giao tuyến của mỗi cặp mặt phẳng sau: (SAD) và (SBC); (MNP) và (ABCD).

Phân tích và Hướng dẫn giải:

1. Giao tuyến $\mathbf{(SAD)}$ và $\mathbf{(SBC)}$: Hai mặt phẳng này có điểm chung $S$. Do đáy $ABCD$ là hình bình hành nên $AD // BC$. Ta áp dụng định lí về giao tuyến song song để tìm giao tuyến.

2. Giao tuyến $\mathbf{(MNP)}$ và $\mathbf{(ABCD)}$: Hai mặt phẳng này có điểm chung $N$. Ta cần tìm một đường thẳng trong $(MNP)$ song song với một đường thẳng trong $(ABCD)$ để áp dụng định lí giao tuyến song song.

Lời giải chi tiết:

Ta có hình minh họa như sau:

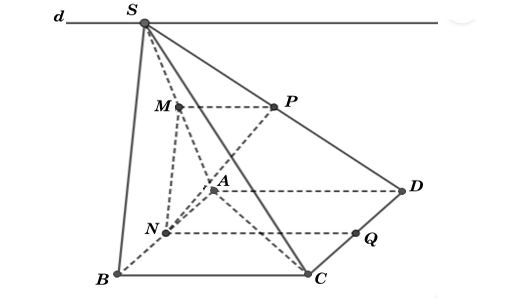
* Xác định giao tuyến của  (SAD) và (SBC)

• Ta có: ABCD là hình bình hành nên AD // BC

Mà AB ⊂ (SAB); BC ⊂ (SBC);

 S ∈ (SAB) và S ∈ (SBC).

Vì vậy giao tuyến của hai mặt phẳng là đường thẳng d đi qua S và song song với AD và BC.

Vậy (SAB) ∩ (SBC) = d.

* Xác định giao tuyến của (MNP) và (ABCD).

• Xét ΔSAD, có: M, P lần lượt là trung điểm của SA, SD

⇒ MP là đường trung bình nên MP // AD.

Mà MP ⊂ (MNP); AD ⊂ (ABCD);

 N ∈ (MNP) và N ∈ (ABCD).

Vì vậy giao tuyến của hai mặt phẳng là đường thẳng đi qua N và song song với AD và BC, cắt CD tại Q.

⇒ (MNP) ∩ (ABCD) = NQ.