Giải bài 5 trang 94 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho MA = 2MS, NS = 2NC.

a) Xác định giao điểm của MN với mặt phẳng (ABC).

b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC).

Phân tích và Hướng dẫn giải:

1. Tìm giao điểm $P = MN \cap (ABC)$ (Phần a):

   • Đường thẳng $MN$ nằm trong mặt phẳng $\mathbf{(SAC)}$.

   • Mặt phẳng $(ABC)$ và mặt phẳng $(SAC)$ có giao tuyến là đường thẳng $\mathbf{AC}$.

   • Giao điểm $P$ chính là giao điểm của $MN$ và giao tuyến $AC$ (vì $AC \subset (ABC)$).

2. Tìm giao tuyến $(BMN) \cap (ABC)$ (Phần b):

   • Hai mặt phẳng đã có điểm chung $\mathbf{B}$ (hiển nhiên).

   • Điểm chung thứ hai chính là giao điểm $\mathbf{P}$ vừa tìm được ở câu a).

   • Giao tuyến là đường thẳng đi qua hai điểm chung đó.

Lời giải chi tiết:

Ta có hình minh hoạ như sau:

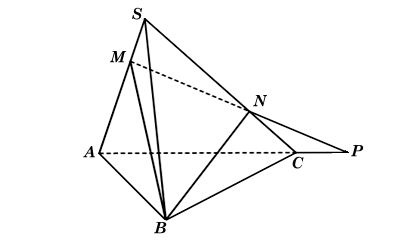
a) Trong mặt phẳng (SAC), gọi giao điểm của MN và AC là P.

Mà AC ⊂ (SAC)

⇒ MN ∩ (ABC) = {P}.

b) Ta có MN ∩ (ABC) = {P} nên P ∈ (ABC)

Lại có P ∈ MN mà MN ⊂ (BMN) nên P ∈ (BMN)

⇒ P là giao điểm của (BMN) và (ABC).

Mặt khác: B ∈ (BMN) và B ∈ (ABC).

⇒ B là giao điểm của (BMN) và (ABC).

Vì vậy (BMN) ∩ (ABC) = BP.