Bài 7.44 trang 65 Toán 11 tập 2 Kết nối tri thức

Bài 7.44 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB // CD và AB = BC = DA = a, CD = 2a. Biết hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) và SA = a. Tính theo a khoảng cách từ S đến mặt phẳng (ABCD) và thể tích của khối chóp S.ABCD.

Kiến Thức Cần Nhớ

• Định lý đường cao: Nếu hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng cũng vuông góc với mặt phẳng đó.

• Hình thang cân: Nắm vững cách tính chiều cao và đường chéo dựa trên tính chất đối xứng.

• Thể tích khối chóp: $V = \frac{1}{3} \cdot S_{đáy} \cdot h$.

Giải bài 7.44 trang 65 Toán 11 Tập 2 Kết nối tri thức:

Ta có hình minh hoạ như sau:

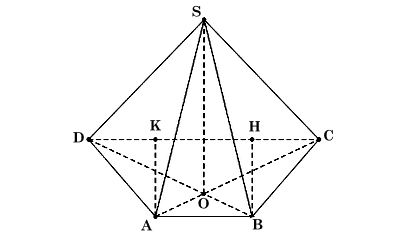
Gọi O là giao điểm của AC và BD.

Vì hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng đáy (ABCD) nên SO ⊥ (ABCD).

Khi đó d(S, (ABCD)) = SO.

Kẻ AH ⊥ DC tại H, BK ⊥ DC tại K.

Khi đó ABKH là hình chữ nhật nên AB = HK = a.

Xét ΔAHD và ΔBKC có:

AD = BC = a,

$\widehat{AHD}=\widehat{BKC}=90^o$

$\widehat{ADH}=\widehat{BCK}$ (vì ABCD là hình thang cân)

Nên ΔAHD = ΔBKC

$\Rightarrow DH+CK=\frac{DC-HK}{2}$ $=\frac{2a-a}{2}=\frac{a}{2}$

CH = HK + KC = a + a/2 = 3a/2

Xét tam giác AHD vuông tại H, có:

$AH=\sqrt{AD^2-DH^2}$ $=\sqrt{a^2-\frac{a^2}{4}}$ $=\frac{a\sqrt{3}}{2}$

Xét tam giác AHC vuông tại H, có:

$AC=\sqrt{AH^2+HC^2}$ $=\sqrt{\frac{3a^2}{4}+\frac{9a^2}{4}}=a\sqrt{3}$

Vì AB // CD nên

$\frac{AO}{OC}=\frac{AB}{CD}$ $\Rightarrow \frac{AO}{OC}=\frac{a}{2a}=\frac{1}{2}$

Suy ra: OC = 2AO

Mà AO + OC = AC nên

$\Rightarrow AO=\frac{1}{3}AC=\frac{a\sqrt{3}}{3}$

Xét tam giác SOA vuông tại O, có:

$SO=\sqrt{SA^2-AO^2}$ $=\sqrt{2a^2-\frac{a^2}{3}}$ $=\frac{a\sqrt{15}}{3}$

Khi đó: $d(S,(ABCD))=\frac{a\sqrt{15}}{3}$

$S_{ABCD}=\frac{1}{2}.(AB+CD).AH$ $=\frac{1}{2}.(a+2a).\frac{a\sqrt{3}}{2}=\frac{3a^2\sqrt{3}}{4}$

Vậy, ta có:

$V_{S.ABCD}=\frac{1}{3}.S_{ABCD}.SO$ $=\frac{1}{3}.\frac{3a^2\sqrt{3}}{4}.\frac{a\sqrt{15}}{3}$ $=\frac{a^3\sqrt{45}}{12}=\frac{a^3\sqrt{5}}{4}$