Bài 7.14 trang 43 Toán 11 tập 2 Kết nối tri thức

Bài 7.14 trang 43 Toán 11 Tập 2 Kết nối tri thức

Trong một khoảng thời gian đầu kể từ khi cất cánh, máy bay bay theo một đường thẳng. Góc cất cánh của nó là góc giữa đường thẳng đó và mặt phẳng nằm ngang nơi cất cánh. Hai máy bay cất cánh và bay thẳng với cùng độ lớn vận tốc trong 5 phút đầu, với các góc cất cánh lần lượt là 10°, 15°. Hỏi sau 1 phút kể từ khi cất cánh, máy bay nào ở độ cao so với mặt đất (phẳng, nằm ngang) lớn hơn?

Chú ý. Độ cao của máy bay so với mặt đất là khoảng cách từ máy bay (coi là một điểm) đến hình chiếu của nó trên mặt đất.

Phân tích Phương pháp Giải

1. Mối quan hệ Quãng đường: Vì hai máy bay có cùng vận tốc và cùng bay trong $1 \text{ phút}$, nên quãng đường bay được của chúng là bằng nhau.

2. Mô hình Hình học: Độ cao $h$ là cạnh đối diện với góc cất cánh $\alpha$ trong một tam giác vuông. Quãng đường $S$ là cạnh huyền.

3. Công thức Độ cao: $\mathbf{h = S \cdot \sin(\alpha)}$.

4. So sánh: So sánh giá trị $\sin(10^\circ)$ và $\sin(15^\circ)$.

Giải bài 7.14 trang 43 Toán 11 Tập 2 Kết nối tri thức

Ta có hình minh hoạ như sau:

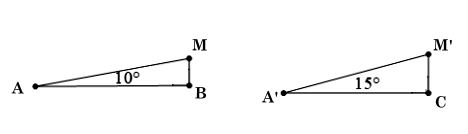
Hai máy bay có cùng độ lớn vận tốc nên sau 1 phút kể từ khi cất cánh hai máy bay bay được quãng đường bằng nhau tức AM = A'M'.

Xét tam giác ABM vuông tại B có BM = AM. sin10°

Xét tam giác A'CM' vuông tại C có CM' = A'M'. sin15°.

Mà sin10° < sin15° nên BM < CM'.

Vậy sau 1 phút cất cánh, máy bay có góc cất cánh 15° ở độ cao lớn hơn so với máy bay có góc cất cánh 10°.