Bài 7.1 trang 30 Toán 11 tập 2 Kết nối tri thức

Bài 7.1 trang 30 Toán 11 tập 2 Kết nối tri thức:

Cho hình lăng trụ ABC.A'B'C' có các y là các tam giác đều. Tính góc (AB, B'C').

Phương Pháp Giải

Để tính góc giữa hai đường thẳng $a$ và $b$ chéo nhau trong không gian, ta thường thực hiện các bước:

1. Tìm một đường thẳng $b'$ sao cho $b' // b$ và $b'$ cắt đường thẳng $a$.

2. Khi đó, góc giữa hai đường thẳng $a$ và $b$ chính là góc giữa hai đường thẳng cắt nhau $a$ và $b'$:

   $(a, b) = (a, b')$

3. Sử dụng các tính chất hình học phẳng (tam giác đều, định lí Cosin,...) để tính độ lớn của góc.

Giải bài 7.1 trang 30 Toán 11 tập 2 Kết nối tri thức:

* Cần nhớ; Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có đường thẳng b' song song với b. Khi đó (a, b) = (a, b')

Ta có hình minh hoạ như sau:

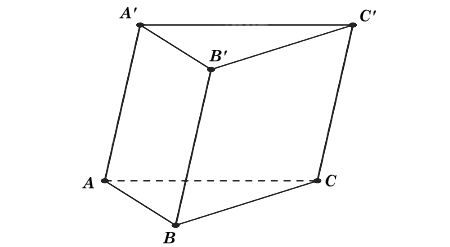
Vì B'C' // BC nên (AB, B'C') = (AB, BC) = $\widehat{ABC}=60^0$ (vì ΔABC đều)